Алгоритмы сжатия данных. Форматы представления данных
Алгоритмы сжатия без потерь. Кодирование
Код Левенштейна. Неравенство Крафта
Кодирование конечных вероятностных источников. Код
Шеннона
Алгоритмы сжатия данных. Форматы представления данных
Код Левенштейна. Неравенство Крафта
Кодирование конечных вероятностных источников. Код
Шеннона
Алгоритмы сжатия данных. Форматы представления данных
Автоматное сжатие. Семейство алгоритмов LZ78 (со
словарем в виде дерева)
Семейство алгоритмов LZ77 (с
использованием исходных данных вместо словаря)
Алгоритм LZSS (=LZ77+признак
прямой записи символа)
Алгоритм LZH (=LZ77+кодирование
длин и смещений алгоритмом Хаффмана)
Алгоритм Deflate
(вариант LZH, использующийся в PKZIP)
Преобразование Барроуза-Уилера (циклический сдвиг
блока)
Алгоритмы сжатия изображений. Форматы представления
изображений
Потоковый ввод-вывод в языке С
Алгоритмы сжатия изображений. Форматы представления
изображений
Потоковый ввод-вывод в языке С
Замечания о представлении чисел в ЭВМ
Графические изображения. Пространства цветов
Алгоритмы сжатия изображений. Форматы представления
изображений
Алгоритмы сжатия изображений с потерями. Форматы
представления изображений
Wavelet – сжатие. Алгоритм JPEG-2000
Шпаргалка для контрольной работы
Алгоритмы сжатия изображений. Форматы представления
изображений
Шпаргалка для контрольной работы
Области видимости и время жизни переменных в языке С
Алгоритмы динамического выделения памяти
Списки блоков фиксированного размера
Алгоритм близнецов (для блоков размером 2k)
Списки блоков свободной памяти в общем случае
Модифицированные списки блоков свободной памяти в
общем случае (алгоритм парных меток)
Объектно-ориентированные языки
Списки блоков свободной памяти в общем случае
Модифицированные списки блоков свободной памяти в
общем случае (алгоритм парных меток)
Объектно-ориентированные языки
Объектно-ориентированные языки
Полиморфизм операционный. Перегрузка операторов и функций
Конструкторы присваивания и копирования*
Недостатки языка С++. Язык Java
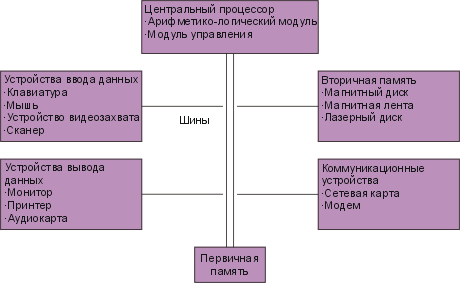
Базовые принципы функционирования вычислительных
систем
Общая конфигурация вычислительной системы
Системные шины на IBM PC – совместимых
комьютерах.
Bus mastering (Управление шиной)
AGP транзакции - адресация по побочной частоте
Организация Кеш-памяти и ассоциативная память в IBM PC-совместимых
ЭВМ
Режимы адресации памяти в Intel-процессорах
Страничная организация памяти в защищенном режиме
Базовые принципы функционирования вычислительных
систем
Режимы адресации памяти в Intel-процессорах
Страничная организация памяти в защищенном режиме
Последовательная обработка данных
Многозадачные пакетные системы
Системы, работающие в режиме разделения времени
Системы реального времени. Многопоточность. Потоки и
процессы
Базовые принципы функционирования вычислительных
систем
Системы реального времени. Многопоточность. Потоки и
процессы
Основные принципы параллельных вычислений
Конкуренция процессов в борьбе за ресурсы
Сотрудничество с использованием разделения
Сотрудничество с использованием связи
Программная реализация. Алгоритм Деккера
Базовые принципы функционирования вычислительных
систем
Программная реализация. Алгоритм Деккера
Программная реализация. Алгоритм Петерсона.
Аппаратная реализация. Отключение прерываний
Аппаратная реализация. Использование машинных команд
Задача о производителях и потребителях
Лекция 1
Алгоритмы сжатия данных. Форматы представления данных
Список литературы
Р.Е. Кричевский. Сжатие и поиск информации. М. Радио и
связь. 1989.
Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин. Методы
сжатия данных. М. Диалог-МИФИ. 2002.
Гюнтер Борн. Форматы данных. Киев. Торгово-издательское бюро BHV. 1995.
Существует два основных типа алгоритмов сжатия:
·
сжатие без потерь (lossless compression)
·
сжатие с потерями (lossy compression)
Рассмотрим сначала алгоритмы сжатия без потерь.
Алгоритмы сжатия без потерь. Кодирование
Имеется некоторый источник данных, выдающий данные в виде слов. Каждое слово состоит из символов или букв некоторого алфавита. Например, слова могут быть некоторыми последовательностями бит заданной длины R, что мы и будем предполагать в дальнейшем.
Существует два принципиально разных вида источников данных комбинаторные и вероятностные. В случае комбинаторных источников известно, что они могут порождать слова только из некоторого набора. Для вероятностных источников такого набора нет, но для каждого слова известно, с какой вероятностью это слово может появиться во входном потоке данных.
Блоком данных будем называть некоторую конечную последовательность слов, выданных источником данных.
Целью задачи сжатия является замена данного блока данных А другим блоком В, по возможности меньшего размера, по которому можно бы было однозначно восстановить исходный блок данных. В этом случае коэффициентом сжатия называется отношение длины блока В (в битах) к длине блока А.
Теорема. Не существует алгоритма сжатия,
который бы для всевозможных блоков А обеспечивал бы коэффициент сжатия
меньше 1.
Доказательство. Рассмотрим все блоки Аi длины N. Таких блоков всего 2N. Если предположить, что для всех этих блоков коэффициент сжатия для данного алгоритма сжатия меньше 1, то получим что среди всех соответствующих блоков Вi (число которых тоже равно 2N) должны обязательно найтись хотя бы два одинаковых. Т.о., мы получили, что для двух одинаковых блоков Вi существуют два различных исходных блока Аi, по этой причине однозначно восстановить исходные блоки по блокам Вi невозможно.
¢
Одним из подходов к проблеме сжатия является кодирование. В процессе кодирования каждый символ входного алфавита заменяется на другой символ, причем наиболее часто встречающиеся символы следует заменять на более короткие символы и наоборот. При этом подходе, кодом называется допустимое множество слов рассматриваемого алфавита. Бинарным кодом называется код, символы которого представляются одним битом.
Определение. Префиксным кодом называется такое множество слов, что ни одно из них не является префиксом другого.
Определение. Код называется дешифруемым, если из любой последовательности допустимых слов без разделителей (=последовательности символов) можно однозначно выделить слова данной последовательности.
Префиксный код по определению является дешифруемым, но не наоборот. Действительно, бинарный код {{0},{0,1}} является дешифруемым (если последовательность бит, полученную при рассмотрении последовательности слов из данного алфавита, перевернуть в обратном порядке и, соответственно, перевернуть в обратном порядке слова данного кода, то мы получим обычный префиксный код), но префиксным данный код не является.
Код Левенштейна. Неравенство Крафта
Было бы интересно получить префиксный код для натуральных чисел. При этом, если бы длина коротких слов была бы меньше длины длинных, то это дало бы возможность использовать его при записи повторителей перед повторяющимися словами. Такой код был придуман Левенштейном.
Его идея довольно проста. Допустим, мы хотим записать код некоторого целого числа x. Запишем все его биты, начиная со старшего значащего. Перед ним запишем длину бинарного представления x (опять, начиная со старшего значащего бита). Перед получившейся последовательностью бит запишем длину длины числа x. И т.д. до тех пор, пока длина очередной длины не станет равной 2. Перед записью этой последней длины запишем 0, а перед ним запишем столько единиц, сколько чисел всего мы записали (имеется в виду само число, его длину, длину длины и т.д.) плюс 1.
Осталось заметить, что старший значащий бит любого положительного числа равен 1, поэтому его можно вообще не писать.
Восстановить исходную информацию можно в обратном порядке. Последовательность единиц в начале (терминирующаяся нулем) определяет количество частей в последующей записи числа. Первая часть состоит из одной цифры (плюс единица старшего разряда `в уме’). Значение первой части задает длину следующей. И.т.д. Последняя часть является требуемым числом.
Будем обозначать код Левенштейна числа x с помощью L(x). Тогда
L(0)
= {0}
L(1)
= {10}
L(2)
= {11 0 0}
L(3)
= {11 0 1}
L(4)
= {111 0 0 00}
…
Заметим, что любой код, кроме кода нуля начинается с 1, поэтому если мы рассматриваем только положительные целые числа, то либо первую единицу можно вообще не писать, либо писать код числа x-1.
Оказывается, что код Левенштейна в некотором смысле оптимален.
Утверждение (неравенство Крафта). Для существования
префиксного кода, состоящего из слов длин l1,…,lN
необходимо и достаточно выполнения следующего неравенства
S1
N 2 -l i £
1
Доказательство.
(<=)
Перепишем неравенство Крафта в следующей форме
S1
lN sk 2
-k £
1
где sk – количество слов
длины k.
Рассмотрим множества слов Zi , состоящие из
всех слов длины i.
Возьмем Z1 и оставим в нем s1 любых слов (это
возможно, т.к. по неравенству s1£
2).
Рассмотрим все Zi (i>1) и исключим из них все слова, начинающиеся на слова, оставшиеся в Z1. Исключенных слов
будет, соответственно, s12i-1 . Из оставшихся в Z2
22- s122-1 слов оставим s2 слов. Это
возможно, т.к.
s1 2 –1+
s2 2
–2 £
1 =>
s2 £ 22- s1 22–1
Рассмотрим все Zi (i>2) и исключим из них все слова, начинающиеся на слова, оставшиеся в Z2. Исключенных слов
будет, соответственно, s22i-2 . Из оставшихся в Z3
23- s123-1-
s223-2 слов оставим s3 слов. Это
возможно, т.к.
s1 2 –1+
s2 2
–2+ s3 2 –3 £
1 =>
s3 £ 23- s1 23–1-
s2 23–2
Т.о. на каждом шаге k мы рассматриваем все Zi (i>k) и исключаем из них все слова, начинающиеся на слова, оставшиеся в Zk. Исключенных слов
будет, соответственно, sk2i-k . Из оставшихся в Zk+1 2k- s12k-1- s22k-2-…- s22k-(k-1) слов оставляем sk слов. Это возможно, т.к.
s1 2 –1+ s2
2 –2+ s3 2 –3+…+ sk 2 –k
£ 1
=> sk £ 2k- s1 2k–1-
s2 2k–2-…- s22k-(k-1)
Т.о. мы построили префиксный код со словами
требуемой длины.
(=>)
Пусть задан некоторый префиксный код.
Рассмотрим все слова длины lN, начинающиеся с каждого слова данного префиксного
кода. По условию, все эти слова различаются. Тогда, их общее число равно S1 N 2 l N –l i (т.к. для каждого слова
префиксного кода таких слов 2 l N –l i). Но общее число
слов длины lN равно 2lN, откуда получаем
S1
N 2 l N –l i£2lN => S1
N 2 -l i £
1
¢
Стоит задаться вопросом: а когда вышеуказанное
неравенство превращается в равенство?
Определение (напоминание). Два
слова a и b называются подобными, если либо a является префиксом b, либо b является
префиксом a.
Лемма 1. Неравенство
Крафта превращается в равенство для множества слов кода Z, тогда и только
тогда, когда любое целое x подобно некоторому слову из Z.
Доказательство. Рассмотрим случай конечного множества слов Z.
(<=)
Пусть M=MAX(li)+1. Рассмотрим все
слова длины M, начинающиеся с
каждого слова данного префиксного кода. По условию, все эти слова различаются.
Тогда, их общее число равно S1
N 2 M –l i (т.к.
для каждого слова префиксного кода таких слов 2 M –l i).
Т.к. никакое слово длины M не может быть префиксом какого либо слова из Z, то, по условию
любое слово длины M имеет префикс, совпадающий с одним из слов из
Z. Но общее число
слов длины M равно 2M, откуда получаем
S1
N 2 M –l i=2M => S1
N 2 -l i = 1
(=>)
Если найдется целое число x, такое что оно не
является подобным ни одному слову из Z, то все слова, начинающиеся со слова x не окажутся
посчитанными в сумме S1
N 2 M –l i, поэтому равенство
не будет выполняться.
Аналогично можно провести доказательство для случая бесконечных множеств слов.
¢
Т.о., в силу алгоритма раскодирования кода
Левенштейна мы получаем, что для кода Левенштейна (в силу алгоритма для любого
целого x оно либо является префиксом некоторого кода Левенштейна, либо некоторый
код Левенштейна является префиксом x) неравенство Крафта превращается в равенство.
Оказывается, что неравенство Крафта верно не
только для префиксных кодов, но и для всех дешифруемых кодов.
Лемма 2. Для слов длин l1,…,lN любого дешифруемого кода
выполняется неравенство
S1
N 2 -l i £
1
Доказательство. Без
доказательства.
¢
Оказывается, что код Левенштейна обладает не
только свойством `глобальной’ оптимальности (см. выше), но и локальной, т.е.
поведение функции скорости роста длины бинарного представления кода числа x от самого числа
нельзя принципиально улучшить.
Заметим, что длина бинарного представления
числа x равна [log2 x] (имеется в виду
собственно бинарное представление, без представления длины числа).
Везде далее если мы не указываем основание
логарифма, то это – двоичный логарифм.
Определим число единичек в начале двоичного
представления код Левенштейна числа x через log*(x). Данная функция растет крайне медленно.
Итак,
|L(x)|=[log(x)]+ [log log (x)]+…+ [log(x)](m) + 1 + log*(x)
здесь под [log(x)](m) имеется в виду m раз применение
функции [log(*)].
Следующая лемма утверждает, что принципиально
улучшить поведение функции скорости роста длины кода числа в зависимости от
значения самого числа невозможно.
Лемма 3. Для слов длин
l1,
l2,… любого дешифруемого кода K с бесконечным числом слов и для любого
заданного целого p следующее неравенство будет выполняться для
бесконечного числа слов:
|L(x)| ³ [log(x)]+ [log log (x)]+…+ [log(x)](p)
Доказательство. Допустим,
это не так. Тогда начиная с некоторого x0 для всех x>x0
|L(x)| < [log(x)]+ [log log (x)]+…+ [log(x)](p)
но ряд
S x0 ¥ 2 –|L(x)| @ S x0 ¥ 1/x 1/log(x) …1/log(p)(x)
расходится (по
интегральному признаку: ò 1/x 1/log(x) …1/log(p)(x) dx = log(p+1)(x)), что сразу же
противоречит неравенству Крафта.
¢
Кодирование конечных вероятностных источников. Код Шеннона
Итак, у нас есть конечный вероятностный
источник S. Т.е. он
порождает слова ai с вероятностью pi. С помощью нашего
дешифруемого префиксного взаимно-однозначного кодирования мы сопоставляем
словам ai код K(ai). В результате мы
можем оценить среднюю длину получившегося кода
C=S pi |K(ai)|
Введем понятие энтропии
H= -S pi log pi
Оказывается, что энтропия дает нижнюю оценку
средней длине получившегося кода. Величина R=C-H называется избыточностью. Верна
Лемма 4. Избыточность дешифруемого кодирования
неотрицательна.
Доказательство.
R=C-H=S pi (|K(ai)|+ log pi)= -S pi log(2-|K(ai)|/pi )
Воспользуемся неравенство Иенсена для выпуклых
вверх функций:
S pi g(xi)£ g(S pi xi)
где S pi =1
тогда имеем:
R= -S pi log(2-|K(ai)|/ log pi )³ - log(S pi 2-|K(ai)|/ pi )= - log(S 2-|K(ai)| ) ³ 0
¢
Шенноном был предложен код, избыточность которого не превышает 1.
Переупорядочим слова, порождаемые источником S, в порядке
убывания вероятностей их появления pi. Т.о., мы будем
иметь:
p1£ p2£…£ pN
Определим суммы
s1= 0
s2= p1
s3= p1+
p2
…
sk= p1+
p2+…+ pk-1
Для кода Шеннона в качестве K(ai) будем брать
первые é-log
più бит двоичного разложения числа sk.
Например
p1=0.5={0.1} é-log p1ù
=1
p2=0.25={0.01} é-log p2ù
=2
p3=0.125={0.001} é-log p3ù =3
p4=0.125/2={0.0001} é-log p4ù =4
p5=0.125/2={0.0001} é-log p5ù =4
тогда
s1=0.0={0.0} K(a1)={0}
s2=0.5={0.1} K(a1)={10}
s3=0.75={0.11} K(a1)={110}
s4=0.875={0.111} K(a1)={1110}
s5=0.125/2={1.1111} K(a1)={1111}
Имеем
|K(ai)| = é-log più
=> |K(ai)| ³ -log pi
=> 2 |K(ai)| ³ 1/ pi =>2 -|K(ai)| £ pi
из чего сразу получаем, что один из первых |K(ai)| бит разложения pi отличен от нуля,
а это гарантирует, что все si различны, т.к. si+1 отличается от si на pi. Т.о., мы
получили, что код Шеннона – префиксный.
Посчитаем среднюю длину кода Шеннона
C=S pi |K(ai)|= S pi é-log più
Избыточность
R=C-H=S pi é-log più +S pi log pi=S pi( é-log più +log pi) £S pi=1
Итак, мы доказали следующую лемму
Лемма 5. Избыточность кода Шеннона не превышает 1.
Код Хаффмана
Преимуществом кода Шеннона является то, что в нем выписываются явные
формулы для кодов исходных слов. Код Хаффмана дает код с минимально возможной
избыточностью среди всех префиксных кодов, но для его вычисления используется
рекурсивная процедура.
Докажем начала следующую лемму.
Лемма 6. Пусть, как мы предполагали изначально, {pi} представляют
собой убывающую последовательность. Утверждается, что для кода с
минимальной избыточностью среди всех префиксных кодов последовательность{|K(si)|} не
убывает и для двух ее последних членов |K(sN-1)| и
|K(sN)| равны.
Более того, последние члены последовательности с равными длинами можно
переупорядочить так, чтобы два последних слова K(sN-1) и
K(sN) совпадали
бы с точностью до последнего бита.
Доказательство.
1)Допустим, что для оптимального кода последовательность {|K(si)|} не является неубывающей, но тогда существуют i < j, такие что |K(si)|> |K(sj)|. Поменяв местами коды слов ai и aj, получим, что длина кода уменьшится, что противоречит оптимальности кода.
2)Допустим, что |K(sN-1)| < |K(sN)|. Из условия префиксности кода имеем, что ни один из K(si) не может быть префиксом K(sN), но тогда мы можем отбросить последний бит из K(sN), сохранив свойство префиксности кода. Получили противоречие с оптимальностью кода.
3)Рассмотрим K(sN). Пусть слово K’(sN) получено из K(sN) путем замены последнего бита на противоположный. Допустим, что не нашлось K(si)= K’(sN) (иначе все доказано). В таком случае мы можем отбросить последний бит из K(sN), не нарушая префиксности кода, т.к., по условию, ни одно из слов длины меньше |K(sN)| не может быть префиксом полученного слова. С другой стороны, полученное слово является префиксом только K(sN).
¢
Лекция 2
Алгоритмы сжатия данных. Форматы представления данных
Список литературы
Р.Е. Кричевский. Сжатие и поиск информации. М. Радио и
связь. 1989.
Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин. Методы
сжатия данных. М. Диалог-МИФИ. 2002.
Гюнтер Борн. Форматы данных. Киев. Торгово-издательское бюро BHV. 1995.
Код Левенштейна. Неравенство Крафта
Оказывается, что
код Левенштейна обладает не только свойством `глобальной’ оптимальности (см.
выше), но и локальной, т.е. поведение функции скорости роста длины бинарного представления
кода числа x от самого числа нельзя принципиально улучшить.
Заметим, что длина
бинарного представления числа x равна [log2 x] (имеется в виду
собственно бинарное представление, без представления длины числа).
Везде далее если
мы не указываем основание логарифма, то это – двоичный логарифм.
Определим число
единичек в начале двоичного представления код Левенштейна числа x через log*(x). Данная функция
растет крайне медленно.
Итак,
|L(x)|=[log(x)]+ [log log (x)]+…+ [log(x)](m) + 1 + log*(x)
здесь под [log(x)](m) имеется в виду m раз применение
функции [log(*)].
Следующая лемма
утверждает, что принципиально улучшить поведение функции скорости роста длины
кода числа в зависимости от значения самого числа невозможно.
Лемма
3. Для слов длин l1, l2,… любого дешифруемого кода K с бесконечным числом слов и для любого
заданного целого p следующее неравенство будет выполняться для
бесконечного числа слов:
|L(x)| ³ [log(x)]+ [log log (x)]+…+ [log(x)](p)
Доказательство. Допустим, это не так. Тогда начиная с
некоторого x0 для всех x>x0
|L(x)| < [log(x)]+ [log log
(x)]+…+ [log(x)](p)
но ряд
S x0 ¥ 2 –|L(x)| @ S x0 ¥ 1/x 1/log(x) …1/log(p)(x)
расходится (по интегральному признаку: ò
1/x 1/log(x) …1/log(p)(x) dx = log(p+1)(x)), что сразу же
противоречит неравенству Крафта.
¢
Кодирование конечных вероятностных источников. Код Шеннона
Итак, у нас есть
конечный вероятностный источник S. Т.е. он порождает слова ai с вероятностью pi. С помощью нашего
дешифруемого префиксного взаимно-однозначного кодирования мы сопоставляем
словам ai код K(ai). В результате мы
можем оценить среднюю длину получившегося кода
C=S pi |K(ai)|
Введем понятие энтропии
H= -S pi log pi
Оказывается, что
энтропия дает нижнюю оценку средней длине получившегося кода. Величина R=C-H называется избыточностью. Верна
Лемма 4. Избыточность
дешифруемого кодирования неотрицательна.
Доказательство.
R=C-H=S pi (|K(ai)|+ log pi)= -S pi log(2-|K(ai)|/pi )
Воспользуемся
неравенство Иенсена для выпуклых вверх функций:
S pi g(xi)£ g(S pi xi)
где S pi =1
тогда имеем:
R= -S pi log(2-|K(ai)|/ pi )³ - log(S pi 2-|K(ai)|/ pi )= - log(S 2-|K(ai)| ) ³ 0
¢
Шенноном был предложен код, избыточность которого не превышает 1.
Переупорядочим слова, порождаемые
источником S, в порядке
убывания вероятностей их появления pi. Т.о., мы будем
иметь:
p1£ p2£…£ pN
Определим суммы
s1= 0
s2= p1
s3= p1+ p2
…
sk= p1+ p2+…+
pk-1
Для кода Шеннона в качестве K(ai) будем брать первые é-log più бит двоичного разложения числа sk.
Например
p1=0.5={0.1} é-log p1ù
=1
p2=0.25={0.01} é-log p2ù
=2
p3=0.125={0.001} é-log p3ù =3
p4=0.125/2={0.0001} é-log p4ù =4
p5=0.125/2={0.0001} é-log p5ù =4
тогда
s1=0.0={0.0} K(a1)={0}
s2=0.5={0.1} K(a1)={10}
s3=0.75={0.11} K(a1)={110}
s4=0.875={0.111} K(a1)={1110}
s5=0.125/2={1.1111} K(a1)={1111}
Имеем
|K(ai)| = é-log più
=> |K(ai)| ³ -log pi
=> 2 |K(ai)| ³ 1/ pi =>2 -|K(ai)| £ pi
из чего сразу получаем, что один из первых |K(ai)| бит разложения pi отличен от нуля,
а это гарантирует, что все si различны, т.к. si+1 отличается от si на pi. Т.о., мы
получили, что код Шеннона – префиксный.
Посчитаем среднюю длину кода Шеннона
C=S pi |K(ai)|= S pi é-log più
Избыточность
R=C-H=S pi é-log più +S pi log pi=S pi( é-log più +log pi) £S pi=1
Итак, мы доказали
следующую лемму
Лемма 5. Избыточность
кода Шеннона не превышает 1.
Код Хаффмана
Преимуществом кода Шеннона является то, что в
нем выписываются явные формулы для кодов исходных слов. Код Хаффмана дает код с
минимально возможной избыточностью среди всех префиксных кодов, но для его
вычисления используется рекурсивная процедура.
Докажем начала следующую лемму.
Лемма 6. Пусть, как мы
предполагали изначально, {pi} представляют собой убывающую
последовательность. Утверждается, что для кода с минимальной
избыточностью среди всех префиксных кодов последовательность{|K(si)|} не
убывает и для двух ее последних членов |K(sN-1)| и
|K(sN)| равны.
Более того, последние члены последовательности с равными длинами можно
переупорядочить так, чтобы два последних слова K(sN-1) и
K(sN) совпадали
бы с точностью до последнего бита.
Доказательство.
1)Допустим, что для оптимального кода последовательность {|K(si)|} не является неубывающей, но тогда существуют i < j, такие что |K(si)|> |K(sj)|. Поменяв местами коды слов ai и aj, получим, что длина кода уменьшится, что противоречит оптимальности кода.
2)Допустим, что |K(sN-1)| < |K(sN)|. Из условия префиксности кода имеем, что ни один из K(si) не может быть префиксом K(sN), но тогда мы можем отбросить последний бит из K(sN), сохранив свойство префиксности кода. Получили противоречие с оптимальностью кода.
3)Рассмотрим K(sN). Пусть слово K’(sN) получено из K(sN) путем замены последнего бита на противоположный. Допустим, что не нашлось K(si)= K’(sN) (иначе все доказано). В таком случае мы можем отбросить последний бит из K(sN), не нарушая префиксности кода, т.к., по условию, ни одно из слов длины меньше |K(sN)| не может быть префиксом полученного слова. С другой стороны, полученное слово является префиксом только K(sN).
¢
Последняя Лемма, фактически, дает алгоритм
построения кода Хаффмана. Процедура имеет рекурсивный характер. Один шаг
заключается в следующем. Упорядочим исходные слова в порядке убывания pi – вероятностей появления соответствующих слов. Для случая оптимального
кода два последних слова в этой последовательности, согласно Лемме, имеют
равную длину кода и отличаются только на последний бит. Поэтому мы можем
объединить их в одно псевдо-слово с суммарной вероятностью появления, равной
сумме вероятностей появления двух исходных слов, и с кодом, состоящим из общих
бит исходных слов (по утверждению Леммы, у этих кодов отличается лишь последний
бит). Следует, конечно, запомнить, что коды двух исходных слов получаются из
кода псевдо-слова добавлением в конец, соответственно, 0 и 1.
Т.о. задача свелась к исходной.
Отметим, что один шаг алгоритма Хаффмана
сводит задачу минимизации
S=S pi |K(ai)|
к задаче минимизации другой величины
S’=S pi’ |K(ai’)|
при этом
S- S’=pN+pN-1
т.к. мы сократили длины двух последних слов на 1 бит, сопоставив им одно слово. Т.о., S и S’ отличаются на константу и задачи их минимизации эквивалентны.
Приведем
пример построения кода Хаффмана. Пусть есть слова из исходного словаря с
вероятностями {0.4, 0.2, 0.15, 0.1, 0.06, 0.05, 0.03, 0.01}.
В одном столбце будем записывать вероятности псевдо-слов на очередном шаге алгоритма. За один шаг сливаются в одно псевдо-слово два последних псевдо-слова из текущего словаря.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0.4
0.4 0.4 0.4 0.4 0.4 0.6
0.4
0.4 0.4 0.4 0.4 0.4 0.6
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]() 0.2
0.2 0.2 0.2 0.25 0.35 0.4
0.2
0.2 0.2 0.2 0.25 0.35 0.4
![]()
![]()
![]()
![]() 0.15
0.15 0.15 0.15 0.2 0.25
0.15
0.15 0.15 0.15 0.2 0.25
![]()
![]()
![]()
![]()
![]() 0.1
0.1 0.1 0.15 0.15
0.1
0.1 0.1 0.15 0.15
![]()
![]()
![]()
![]() 0.06
0.06 0.09 0.1
0.06
0.06 0.09 0.1
![]() 0.05
0.05 0.06
0.05
0.05 0.06
![]()
![]() 0.03
0.04
0.03
0.04
0.01
При восстановлении требуемого кода мы сопоставляем двум последним пседо-словам коды 0 и 1, соответственно. Далее, от каждого псевдо-слова текущего словаря по направлению, обратному движению стрелок, мы переходим к предыдущему словарю. При этом, если с данной псевдо-слово приходит одна стрелка, то мы просто переносим текущий код на предыдущее псевдослово. А если стрелок две, то мы переносим текущее псевдо-слово, дописывая в его конец 0 и 1, соответственно.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0
0 0 0 0 0 1
0
0 0 0 0 0 1
![]()
![]()
![]()
![]()
![]()
![]()
![]() 10
10 10 10 10 11 0
10
10 10 10 10 11 0
![]()
![]()
![]()
![]()
![]()
![]() 110 110 110 110 111 10
110 110 110 110 111 10
![]()
![]()
![]()
![]()
![]() 1110 1110 1110 1111 110
1110 1110 1110 1111 110
![]()
![]()
![]()
![]() 11110 11110 11111 1110
11110 11110 11111 1110
![]() 111111 111111 11110
111111 111111 11110
![]()
![]() 1111101 111110
1111101 111110
1111100
Получили, что теперь средняя длина одного
слова есть
0.4*1+ 0.2*2+ 0.15*3+ 0.1*4+ 0.06*5+ 0.05*6+ 0.03*7+ 0.01*7=2.53
Исходных код требовал 3 бита на слово. Энтропия:
H=-S pi log pi≈2.41373
Избыточность:
C-H ≈0.11627
Сжатие с помощью стопки книг
Алгоритм Хаффмана требует знания вероятностей появления отдельных слов. В реальности это значит, что для его прямого применения необходимо сначала получить все слова сжимаемого блока данных, посчитать сколько раз в блоке встречается каждое слово и только потом реализовывать сам алгоритм. Алгоритм сжатия с помощью стопки книг является адаптивным. Т.е. он не требует априорного знания вероятностей появления отдельных слов. Вместо этого, код каждого слова изменяется при поступлении каждого нового слова из источника данных. При этом, последнее пришедшее слово получает самый короткий код.
Код K называется монотонным, если функция K(x) является монотонно возрастающей.
Пусть задан некоторый произвольный монотонный префиксный код K. Если размер исходного словаря не ограничен, то, например, можно использовать код Левенштейна (легко показать, что код Левенштейна - монотонен). Отметим, что из монотонности кода следует, что функция |K(x)| тоже монотонна (не строго).
На источнике и приемнике данных заведем одинаковою таблицу T, в которой, изначально, в ячейке i располагается текущее слово словаря ai . Будем полагать, что слову, расположенному в ячейке таблицы T с номером i сопоставляется код K(i). Т.о. длина кода всегда будет монотонной функций от номера ячейка. При передаче очередного слова будем искать это слово в таблице (допустим, слово размещается в ячейке с номером i) и передавать его код, определенный на текущий момент (т.е. K(i)). После этого, слово из ячейки i переносится в первую ячейку таблицы, а часть таблицы с первой по i-1 позицию, соответственно, сдвигается на одну позицию впрваво:
tmp=T[i];
for(j=i-1;j>=0;j++)T[j+1]=T[j];
T[0]=tmp;
При этом, часто встречающиеся слова будут группироваться в области меньших номеров таблицы, и, соответственно, будут иметь меньшую длину кода.
Отметим, что прямая реализация `стопки книг’ оказывается весьма дорогой, т.к. если реализовать ее в виде массива, то каждая из операций поиска слова в таблице и переноса слова в начало таблицы будут занимать время O(N), где – N размер массива.
`Стопку книг’, например, можно реализовать с помощью двух сбалансированных бинарных деревьев, в которых дополнительно хранятся информация о порядковом номере каждого элемента (напомним, что такую информацию можно хранить, поместив в каждую вершину число, равное количеству вершин дерева в левом поддереве, выходящем из данной вершины). Первое дерево будет задавать саму таблицу, используемую в алгоритме, а второе дерево будет содержать уже появившееся слова в лексикографическом порядке. Т.о. каждому слову будет соответствовать по одной вершине в каждом дереве. Между соответствующими вершинами должны быть ссылки друг на друга.
Если появляется очередное слово, то мы ищем его во втором дереве (в силу упорядоченности слов, это можно сделать за O(logN) операций). Если слово найдено в дереве, то берем соответствующую вершину в первом дереве и перемещаем ее на первую позицию в дереве (т.е. исключаем вершину из первого дерева и помещаем в самую левую позицию, проводя все необходимые балансировки). Это также потребует O(logN) операций. Если слово не найдено в дереве, то вставляем его во второе дерево и соответствующую вершину вставляем на первую позицию в первом дереве.
Т.о., кодирование методом стопки книг можно реализовать за время O(logN), где N – количество слов входной последовательности.
Автоматное сжатие
Напомним, что Конечным автоматом ранее мы называли объект, состоящий из пяти множеств:
Q – конечное множество состояний;
AÌ Q – подмножество принимающих состояний;
q0Î
Q – начальное состояние;
S
– конечный входной алфавит;
d: Q ´ A ® Q – функция перехода.
Добавим к этому понятию функцию g: : Q ´ A ® {0,1}*, сопоставляющую состоянию и символу некоторую, возможно пустую, последовательность букв выходного алфавита (т.е., в нашем случае, последовательность из нулей и единиц). Будем называть эту функцию выходной.
Предполагается, что функция перехода вычисляется за время O(1), т.к. обычно она задается таблицей.
Рассмотрим следующий алгоритм. Пусть источник данных выдает последовательность букв {x[i]}. Выделим из нее подряд идущие подпоследовательности букв Xi={x[ni+1] ,…, x[ni+1]}, такие что каждая подпоследовательность это - кратчайшая подпоследовательность, начинающаяся с x[ni+1], которая не совпадает ни с одной Xj , j<i. Например:
0
01 1 10 11 111 1111
101 1011
Заметим, что для каждого слова длины больше 1 если из слова отбросить последнюю букву, то остаток должен обязательно встретиться среди предыдущих слов. Пусть функция p(i) задает номер слова, равного слову Xi без последней буквы. Имеем: p(i)<i.
Тогда для кодирования каждого слова этой последовательности Xi достаточно указывать значение функции p(i) и последнюю букву слова Xi , т.е.. Будем кодировать слово Xi с помощью числа
K(Xi )
= p(i)|S| + x[ni+1]
Здесь мы предполагаем, x[ni+1] задается своим порядковым номером (начиная с 0), |S| - количество символов в алфавите. Имеем
K(Xi ) = p(i)|S| + x[ni+1] ≤ (i-1) |S| + |S|-1=i |S| -1
Т.о. для задания K(Xi ) достаточно élog(i |S|)ù бит. Суммарный размер получившегося кода равен для случая, когда мы имеем M подслов
L(x)=S1M+1 élog(i |S|)ù ≤ M log(M |S|)(1+o(1)) (по интегральному признаку)
Введем понятие продукционной сложности слова x. Продукционной сложностью слова x назовем максимально возможное количество различных подслов, на которое можно разбить слово x. Продукционная сложность не меньше числа подслов {Xi }, используемых выше. Тогда сразу получаем
L(x) ≤ C(x) log(C(x) |S|)(1+o(1))
Можно доказать, что для любого алгоритма кодирования, основанного на конечных автоматах данное соотношение также выполняется.
Осталось показать, что приведенный алгоритм можно реализовать с помощью конечных автоматов.
Пусть выходная функция при поступлении каждого символа выдает пустую строку, если очередное слово Xi еще не выведено полностью, иначе она должна выдавать K(Xi ).
Пусть в данный момент уже выданы коды слов X1 , …, Xi-1 и мы получаем от источника очередной символ xk.
Состояние системы будет характеризоваться номером l слова {x[ni-1+1],…, x[nk-1]} в последовательности подслов { Xj }.
Для быстрого определения номера слова {x[ni-1+1],…, x[nk]}= { Xl, x[nk]} в последовательности подслов { Xj } заведем бинарное дерево, каждая ветка которого задает некоторое слово Xj. В каждое вершине этого дерева будет также хранить номер слова, задаваемого вершинами дерева из ветки, завершающейся на эту вершину. В каждый момент мы будем хранить текущую вершину, задающую состояние системы.
Тогда если у текущей вершины есть потомок со значением x[nk], то этот потомок станет следующим состоянием системы и функция g будет выдавать пустую последовательность символов. Если же такого потомка нет, то функция g должна подать на выход значение K(Xi ) (это не составляет проблем, т.к. значение функции p(i) хранится в текущей вершине), после чего состояние системы должно перейти к пустому слову.
Легко увидеть, что вычисление функций d, g будет требовать времени O(1).
Лекция 3
Алгоритмы сжатия данных. Форматы представления данных
Список литературы
Р.Е. Кричевский. Сжатие и поиск информации. М. Радио и
связь. 1989.
Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин. Методы
сжатия данных. М. Диалог-МИФИ. 2002.
Гюнтер Борн. Форматы данных. Киев. Торгово-издательское бюро BHV. 1995.
Алгоритмы LZ
Алгоритмы Зива-Лемпела (Ziv-Lempel) появились во второй половине 70-х гг. в результате работ Зива и Лемпела. Можно говорить о двух подклассах этих алгоритмов – LZ77 и LZ78.
Принято, что имена конкретных алгоритмов из данной серии получаются путем приписывания одной или нескольких букв имен авторов в конец слова LZ.
Автоматное сжатие. Семейство алгоритмов LZ78 (со словарем в виде дерева)
Напомним, что Конечным автоматом ранее мы называли объект, состоящий из пяти множеств:
Q – конечное множество состояний;
AÌ Q – подмножество принимающих состояний;
q0Î
Q – начальное состояние;
S
– конечный входной алфавит;
d: Q ´ A ® Q – функция перехода.
Добавим к этому понятию функцию g: : Q ´ A ® {0,1}*, сопоставляющую состоянию и символу некоторую, возможно пустую, последовательность букв выходного алфавита (т.е., в нашем случае, последовательность из нулей и единиц). Будем называть эту функцию выходной.
Предполагается, что функция перехода вычисляется за время O(1), т.к. обычно она задается таблицей.
Рассмотрим следующий алгоритм. Пусть источник данных выдает последовательность букв {x[i]}. Выделим из нее подряд идущие подпоследовательности букв Xi={x[ni+1] ,…, x[ni+1]}, такие что каждая подпоследовательность это - кратчайшая подпоследовательность, начинающаяся с x[ni+1], которая не совпадает ни с одной Xj , j<i. Например:
0
01 1 10 11 111 1111
101 1011
Заметим, что для каждого слова длины больше 1 если из слова отбросить последнюю букву, то остаток должен обязательно встретиться среди предыдущих слов. Пусть функция p(i) задает номер слова, равного слову Xi без последней буквы. Имеем: p(i)<i.
Тогда для кодирования каждого слова этой последовательности Xi достаточно указывать значение функции p(i) и последнюю букву слова Xi , т.е.. Будем кодировать слово Xi с помощью числа
K(Xi )
= p(i)|S| + x[ni+1]
Здесь мы предполагаем, x[ni+1] задается своим порядковым номером (начиная с 0), |S| - количество символов в алфавите. Имеем
K(Xi ) = p(i)|S| + x[ni+1] ≤ (i-1) |S| + |S|-1=i |S| -1
Т.о. для задания K(Xi ) достаточно élog(i |S|)ù бит. Суммарный размер получившегося кода равен для случая, когда мы имеем M подслов
L(x)=S1M+1 élog(i |S|)ù ≤ M log(M |S|)(1+o(1)) (по интегральному признаку)
Введем понятие продукционной сложности слова x. Продукционной сложностью слова x назовем максимально возможное количество различных подслов, на которое можно разбить слово x. Продукционная сложность не меньше числа подслов {Xi }, используемых выше. Тогда сразу получаем
L(x) ≤ C(x) log(C(x) |S|)(1+o(1))
Можно доказать, что для любого алгоритма кодирования, основанного на конечных автоматах данное соотношение также выполняется.
Осталось показать, что приведенный алгоритм можно реализовать с помощью конечных автоматов.
Пусть выходная функция при поступлении каждого символа выдает пустую строку, если очередное слово Xi еще не выведено полностью, иначе она должна выдавать K(Xi ).
Пусть в данный момент уже выданы коды слов X1 , …, Xi-1 и мы получаем от источника очередной символ xk.
Состояние системы будет характеризоваться номером l слова {x[ni-1+1],…, x[nk-1]} в последовательности подслов { Xj }.
Для быстрого определения номера слова {x[ni-1+1],…, x[nk]}= { Xl, x[nk]} в последовательности подслов { Xj } заведем бинарное дерево, каждая ветка которого задает некоторое слово Xj. В каждое вершине этого дерева будет также хранить номер слова, задаваемого вершинами дерева из ветки, завершающейся на эту вершину. В каждый момент мы будем хранить текущую вершину, задающую состояние системы.
Тогда если у текущей вершины есть потомок со значением x[nk], то этот потомок станет следующим состоянием системы и функция g будет выдавать пустую последовательность символов. Если же такого потомка нет, то функция g должна подать на выход значение K(Xi ) (это не составляет проблем, т.к. значение функции p(i) хранится в текущей вершине), после чего состояние системы должно перейти к пустому слову.
Легко увидеть, что вычисление функций d, g будет требовать времени O(1).
Данный алгоритм был опубликован в 1978г. Он стал основой большого семейства алгоритмов сжатия.
Семейство алгоритмов LZ77 (с использованием исходных данных вместо словаря)
Первая публикация, посвященная данному алгоритму появилась в 1977г., хотя сам алгоритм был разработан ранее. Это самый старый алгоритм из семейства LZ. В этом алгоритме нет отдельно оформленного словаря появившихся слов, используемых для кодировки следующего куска входных данных. Вместо него используется весь массив уже закодированных данных или его последняя часть.
Источник выдает данные в виде последовательности символов. В данном алгоритме используется окно входных данных длины N символов. Из них W символов относятся к уже закодированной части данных (т.е. их код уже записан в выходной поток), а стальные– к незакодированной. Пусть на входе подается последовательность символов si. Пусть символы st-W ,… , st-1 уже закодированы.
Для нахождения продолжения кода последовательности ищется подстрока { st , st+1 ,… , st+k} (k< N-W ) максимальной длины, совпадающая с некоторой подпоследовательностью символов, которая расположена в данном окне и находится до подстроки { st , st+1 ,… , st+k}.
Более формально. Ищется максимальное k< N-W, такое что существует i (t-W ≤ i < t), для которого строки { st , st+1 ,… , st+k} и { si , si+1 ,… , si+k} совпадают.
На выход подается смещение к найденной строке (= t-i ), длина найденной строки (= k ) и символ st+k+1. Если найденных строк несколько, то берется строка с минимальным значением смещения t-i. Смещение 0 можно зарезервировать для признака конца блока.
Пример. Длина окна=7.
папа_у_васи_силен_в_математике
папа_у_васи_силен_в_математике
1 0 п
папа_у_васи_силен_в_математике
1 0 а
папа_у_васи_силен_в_математике
2 2 _
папа_у_васи_силен_в_математике
1 0 у
папа_у_васи_силен_в_математике
2 1 в
папа_у_васи_силен_в_математике
4 1 с
папа_у_васи_силен_в_математике
1 0 и
папа_у_васи_силен_в_математике
5 1 с
папа_у_васи_силен_в_математике
1 0 и
папа_у_васи_силен_в_математике
1 0 л
папа_у_васи_силен_в_математике
1 0 е
папа_у_васи_силен_в_математике
1 0 н
папа_у_васи_силен_в_математике
6 2 _
папа_у_васи_силен_в_математике
1 0 м
папа_у_васи_силен_в_математике
1 0 а
папа_у_васи_силен_в_математике
1 0 т
папа_у_васи_силен_в_математике
1 0 е
папа_у_васи_силен_в_математике
4 3 и
папа_у_васи_силен_в_математике
1 0 к
папа_у_васи_силен_в_математике
6 1 е
Итого 20 записей, в каждой из которых 3 бита отводится на смещение + 3 бита отводим под буфер предварительного просмотра (вообще говоря, его длину можно было сделать и больше) + 8 бит на символ = 14 бит.
Итого код занимает 14*20=280 бит. Против 30*8=240 бит в исходной строке. Т.о. сжатия мы не получили (коэффициент сжатия > 1). В реальности этот алгоритм, действительно, плохо работает на небольших последовательностях данных.
Проблемой алгоритма LZ77 является потенциальная возможность наличия большого количества ситуаций, когда первый незакодированный символ встречается в последовательности первый раз.
Алгоритм LZSS (=LZ77+признак прямой записи символа)
Простейшей модификацией алгоритма LZ77 является алгоритм LZS, в котором перед каждым записываемым кодом пишется бит, указывающий на то, что далее будет следовать либо просто один символ, либо код, аналогичный вышеописанному. Т.о., в вышеприведенном примере на каждый код добавляется 1 бит, но в ситуациях, когда очередной символ в последовательности данных ранее не встречался код сокращается на 6 бит (смещение и длина не пишутся). Итого, предыдущий пример будет выглядеть следующим образом
папа_у_васи_силен_в_математике
1
п
папа_у_васи_силен_в_математике
1
а
папа_у_васи_силен_в_математике
0 2 2 _
папа_у_васи_силен_в_математике
1
у
папа_у_васи_силен_в_математике
0 2 1 в
папа_у_васи_силен_в_математике
0 4 1 с
папа_у_васи_силен_в_математике
1
и
папа_у_васи_силен_в_математике
0 5 1 с
папа_у_васи_силен_в_математике
1
и
папа_у_васи_силен_в_математике
1
л
папа_у_васи_силен_в_математике
1
е
папа_у_васи_силен_в_математике
1
н
папа_у_васи_силен_в_математике
0 6 2 _
папа_у_васи_силен_в_математике
1
м
папа_у_васи_силен_в_математике
1 а
папа_у_васи_силен_в_математике
1
т
папа_у_васи_силен_в_математике
1
е
папа_у_васи_силен_в_математике
0 4 3 и
папа_у_васи_силен_в_математике
1
к
папа_у_васи_силен_в_математике
0 6 1 е
Итого код занимает 280+20-6*13=222 бит. Против 30*8=240 бит в исходной строке. Т.о. коэффициент сжатия =222/240.
Алгоритм LZH (=LZ77+кодирование длин и смещений алгоритмом Хаффмана)
Алгоритм LZH является естественной модификацией алгоритма LZ77. В нем используется код Хаффмана для сжатия смещений и длин повторяющихся последовательностей, появляющихся в алгоритме LZ.
Алгоритм Deflate (вариант LZH, использующийся в PKZIP)
Известный архиватор PKZIP использует некоторую модификацию алгоритма LZH. Дадим лишь общее описание данного алгоритма, не вдаваясь в подробности.
Каждая последующая порция кода в нем записывается либо в виде {длина, смещение,символ} либо в виде {символ}, где под символом подразумевается 8-битное слово. Для объединения этих двух форм записи вводится алфавит, состоящий из 286 символов. Первые 256 символов отводятся под кодирование одного 8-битного слова, код 256 отводится под признак конца блока, а символы с кодами от 257 до 285 – под кодирование длины. Естественно, что данный символ имеет длину более 8 бит.
Т.о. если требуется напрямую закодировать одно 8-битное слово, то пишется символ с кодом, равным значению данного 8-битного слова. Если требуется задать ссылку на уже встретившийся кусок кода, то сначала записывается длина этого куска. При этом, для длин 3,4,…,10 используются коды 257,258,264. Если требуется закодировать длину 11 или 12, то записывается код 265, после чего дописывается еще один дополнительный бит, уточняющий значение длина (0 соответствует длине 11, а 1 – длине 12). Все дальнейшие кодировки длин строятся аналогичным образом: число из созданного выше алфавита задает диапазон значений длины, а последующие дополнительные биты уточняют длину. Количество дополнительных бит определяется значением символа из созданного алфавита, называемого, в этой ситуации базой.
Итак, длина кодируется в виде базы и некоторого количества дополнительных бит, число которых задается значением базы. Смещение кодируется аналогичным способом: в виде базы и некоторого количества дополнительных бит.
Наконец, полученные выше коды сжимаются, если это эффективно, либо фиксированным кодом Хаффмана (сам код задается заранее, т.е. является стандартным), либо классическим кодом Хаффмана, требующим передачи частот появления различных символов во входном потоке.
Для фиксированного кода используется код, в котором для кодирования слов с номерами от 0 до 143 используется 8 бит, от 144 до 255 – 9 бит, от 256 до 279 – 7 бит, от 280 до 287 – 8 бит.
Для классического кода Хаффмана перед самим кодом записывается таблица данного кода (на самом деле, при ее написании также используется сжатие методом Хаффмана).
Преимуществом данного подхода является наличие широкого выбора алгоритмов сжатия, при которых данные можно разархивировать, пользуясь одной и той же процедурой. Все алгоритмы сжатия могут отличаться способом поиска наиболее длинного слова во входной последовательности символов в уже закодированной информации. Один из таких алгоритмов это – метод хеш-цепочек.
Метод хеш-цепочек заключается в следующем. Сопоставим каждому символу из блока входных данных два указателя – prev и next. С их помощью объединим символы блока входных данных в цепочки, элементы каждой из которых имеют одно значение некоторой хеш-функции. Для каждого символа хеш-функция будет вычисляться по значению этого символа и двух последующих. Тогда при рассмотрении очередной порции символов, генерируемых источником данных, мы будем считать значение той же хеш-функции для первых трех символов этой порции и будем осуществлять поиск наибольшего совпадающего слова среди слов, начинающихся на символы из соответствующей цепочки.
В качестве хеш-функции используется функция, которая может быть посчитана при вводе каждого последующего символа по предыдущему значению функции и по значению нового символа:
int hash(int
LastValue, unsigned char c)
{
return
((LastValue<<H_SHIFT)^c)&HASH_MASK;
}
Легко увидеть, что значение данной хеш-функции не может превзойти HASH_MASK.
Если цепочка достигла большой длины, то ее следует укоротить, но, естественно, это надо делать за счет давно внесенных в нее элементов. Это можно делать, исключая последние элементы цепочки. При этом предполагается, что включать вновь полученное слово в цепочку следует в начало списка.
Одним из вариантов улучшения данного алгоритма является вариант ``ленивого’’ сравнения. Для него мы сначала находим наиболее длинное встретившееся слово, совпадающее со словом, начинающимся на символ st , затем сразу находим наиболее длинное встретившееся слово, совпадающее со словом, начинающимся на символ st+1. Если второе слово оказалось длиннее, то символ st выводится в выходной поток как просто символ и процедура повторяется для st+1.
Арифметическое сжатие
Арифметическое сжатие основано на весьма красивой идее. Пусть на входе нашего алгоритма подаются символы входной последовательности {ai}, появляющиеся с вероятностями {pi} (i=1,…,N). Под символами входной последовательности будем подразумевать натуральные числа от 1 до M.
Разобьем полуинтервал [0,1) на интервалы с длинами pi и сопоставим первому символу из входной последовательности a1 интервал с номером a1 – [x1,y1).
Разобьем далее полуинтервал [x1,y1) на интервалы с длинами (y1 - x1)pi и сопоставим второму символу из входной последовательности a2 интервал из последнего разбиения с номером a2 – [x2,y2].
И.т.д. На каждом шаге разбиваем полуинтервал [xi-1,yi-1) на интервалы с длинами (yi-1 – xi-1)pi и сопоставляем очередному символу из входной последовательности ai интервал из последнего разбиения с номером ai – [xi,yi).
Кодом всей последовательности исходных символов является наикратчайшее число в двоичной системе представления изо всех чисел, находящихся в полуинтервале [xN,yN).
Легко увидеть, что длина конечного интервала равна |xN,yN|=П pi . Тогда, если |xN,yN|≥2-K, то на полуинтервале [xN,yN) обязательно найдется число, в двоичной системе представления которого после K-ой цифры после запятой идут лишь нули.
Действительно, если для числа xN после K-ой цифры после запятой идут лишь нули, то все доказано. Иначе рассмотрим K первых цифр после запятой двоичного представления числа xN и к получившемуся числу xN’ прибавим 2-K. Имеем: xN -xN’>2-K, следовательно xN >xN’+2-K, а в силу того, что |xN,yN|≥2-K плучаем: xN’< yN . Что и требовалось доказать.
Т.о., для случая |xN,yN|=2-K получаем, что длина кода
L= -log|xN,yN|=-log
П pi=
-S1N log pi.
Если мы имеем на входе N символов, то в качестве вероятностей можно рассмотреть величины pj=sj /N, где sj – количество появлении символа j во входном потоке данных. Тогда длину кода можно выписать иначе:
L = -S1M sj log pj.
И для средней длины кодирования одного символа получаем:
L/N = -S1M sj /N log pj = -S1M pj log pj= H
Т.е. в случае |xN,yN|=2-K в точности достигается значение энтропии.
Легко увидеть, что в произвольном случае избыточность не превышает 1/N. А это существенно лучше, чем в алгоритме Хаффмана, где максимальная избыточность может быть сколь угодно близкой к 1 (с одной стороны, см. Пример, а с другой – больше 1 она быть не может, т.к. существует код Шеннона, избыточность которого не превышает 1).
Пример. Во входной последовательности данных символ a встречается 1 раз, а символ b встречается N-1 раз. Код Хаффмана требует 1 бит для кодирования одного символа.
Длина кода L=N. Средняя длина одного символа =1.
Энтропия
H=-(N-1) /N log((N-1)/N)-1/N log(1/N)=- (N-1)/N log(1-1/N)) + 1/N log(N) @
@(N-1)/N2 + 1/N log(N) @ 1/N log(N)® 0
(N®¥)
Избыточность H-L @ 1- 1/N log(N)® 1 (N®¥)
Закодируем последовательность {a,b,…,b} (b встречается N-1 раз)методом арифметического сжатия.
Символ a дает
интервал [1/N, 1).
Символ b дает
интервал [1/N,1/N+((N-1)/N)2).
…
Символ b дает
интервал [1/N,1/N+((N-1)/N)N).
Лекция 4
Алгоритмы сжатия данных.
Список литературы
Р.Е. Кричевский. Сжатие и
поиск информации. М. Радио и связь. 1989.
Д. Ватолин, А. Ратушняк, М.
Смирнов, В. Юкин. Методы сжатия данных. М. Диалог-МИФИ. 2002.
Гюнтер Борн. Форматы данных. Киев. Торгово-издательское бюро BHV. 1995.
Адаптивный алгоритм Хаффмана
В данном разделе мы будем строить дерево Хаффмана не с помощью вероятностей символов, а с помощью числа появлений символов во входном потоке. Ясно, что данная модификация всего лишь умножает все числа в дереве на общее количество символов во входном потоке и ничего не изменяет ни в алгоритме, ни в конечном коде.
Идея адаптивного алгоритма Хаффмана логично вытекает из исходного алгоритма. Вместо того, чтобы хранить таблицу появлений различных символов, давайте сделаем ее динамической. В начальный момент можно задать все вероятности равными, т.е. в таблице частот появлений символов в каждую ячейку мы можем поместить 1. Далее, при поступлении каждого следующего символа мы
1. выводим его код Хаффмана в соответствии с деревом кода Хаффмана
2. увеличиваем на 1 число появлений данного символа в таблице частот появлений символов
3. модифицируем дерево Хаффмана в соответствие с новой таблицей частот
Разархивацию данных производим аналогично (важно, что дерево Хаффмана модифицируется уже после занесения кода символа в выходной поток данных, поэтому при разархивации мы сначала извлекаем символ, а потом модифицируем дерево Хаффмана).
Данный алгоритм слишком медленно работает. Но его несложно модифицировать так, чтобы процедура исправления дерева (только она тормозит процесс) выполнялась бы достаточно быстро.
Напомним
приведенный ранее пример построения кода фиксированного Хаффмана для случая 100
входных символов. Пусть есть слова из исходного словаря с количеством их
появлений {40, 20, 15, 10, 6, 5, 3, 1}.
В одном столбце будем записывать количество псевдо-слов на очередном шаге алгоритма. За один шаг сливаются в одно псевдо-слово два последних псевдо-слова из текущего словаря.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 40
40 40 40 40 40 60
40
40 40 40 40 40 60
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]() 20
20 20 20 25 35 40
20
20 20 20 25 35 40
![]()
![]()
![]()
![]() 15
15 15 15 20 25
15
15 15 15 20 25
![]()
![]()
![]()
![]()
![]() 10
10 10 15 15
10
10 10 15 15
![]()
![]()
![]()
![]() 6
6 9 10
6
6 9 10
![]() 5
5 6
5
5 6
![]()
![]() 3
4
3
4
1
Пусть на данный момент (введено 100 символов) мы имеем указанное дерево. Пусть мы получили еще один символ во входом потоке данных и пусть, для определенности, это – самый редко встречающийся символ. Покажем, как модифицировать построенное дерево для новых вероятностей.
Итак, мы добавляем 1 к соответствующему числу в первом столбце и, соответственно, рекурсивно модифицируем значение родительской вершины:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 40
40 40 40 40 40 61
40
40 40 40 40 40 61
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]() 20
20 20 20 25 35 40
20
20 20 20 25 35 40
![]()
![]()
![]()
![]() 15
15 15 15 20 25
15
15 15 15 20 25
![]()
![]()
![]()
![]()
![]() 10
10 10 16 15
10
10 10 16 15
![]()
![]()
![]()
![]() 6
6 10 10
6
6 10 10
![]() 5
5 6 ???
5
5 6 ???
![]()
![]() 3
5
3
5
2
Данное дерево не является деревом Хаффмана, но в ситуации, когда над исправленным числом стоит число не меньше исправленного ничего менять вообще не нужно, т.к. условие упорядоченности столбцов на рисунке сохраняется.
Если это не так (четвертый столбец слева в примере), то нужно поменять местами измененную вершину v’= v+1 (здесь и далее в формулах вершина и ее значение будут отождествляться) с самой верхней вершиной со значением, равным v (числа во всех вершинах целые, из чего следует что после обмена местами указанных вершин, над новой позицией вершины стоит число не менее v):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 40
40 40 40 40 40 61
40
40 40 40 40 40 61
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]() 20
20 20 20 25 36 40
20
20 20 20 25 36 40

![]()
![]()
![]()
![]()
![]() 15
15 15 16 20 25
15
15 15 16 20 25
![]()
![]()
![]() 10
10 10 15 16
10
10 10 15 16
![]()
![]()
![]()
![]() 6
6 10 10
6
6 10 10
![]() 5
5 6
5
5 6
![]()
![]() 3
5
3
5
2
Объясним, почему должна произойти именно эта замена. Пусть длина кода для измененной вершины v равна m, длина кода для вершины, с которой мы хотим поменять ее местами, равна l. Тогда уменьшение длины суммарного кода при перестановке данных вершин равно
D= ((v+1)m+ vl) - ((v+1)l+
vm) =(v+1)(m-l) – v(m-l)=m-l
Т.о. для обмена нам следует выбрать вершину с минимальным l среди вершин с
длиной кода равной v.
Т.к. при обмене местами двух вершин смещаться мы будем
только вверх, то суммарное количество операций по обмену местами вершин не
будет превышать M,
где M =количеству слов в исходном словаре. Т.о.
максимальное время, затрачиваемое на кодирование одного слова, равно O(M) .
Контекстное сжатие
Идея метода появилась в публикации в 1981г.
При описании алгоритмов контекстного сжатия следует выделить две составляющих: контекстное моделирование и собственно кодирование.
В процессе контекстного моделирования происходит оценка вероятности появления текущего символа, исходя из информации об уже закодированных данных. На этапе кодирования выполняется собственно процесс сжатия на основе полученной информации о вероятностях появления символов из статистической модели данных, полученной на этапе контекстного моделирования.
Действительно, например, если мы знаем, что декодируем текст русского языка, то количество букв, которые могут следовать после строки `строк’ не так уж и велико, чем можно воспользоваться при сжатии текста.
Контекстом символа xi будем называть последовательность символов, предшествующих xi (вообще говоря, существуют левосторонние и правосторонние контексты; мы будем пользоваться лишь левосторонними контекстами).
Контекстом порядка N символа xi будем называть последовательность из N символов, предшествующих xi : { xi-N ,…, xi-1 }. Контекстом моделированием порядка N будем называть построение таких моделей, которые для оценки появления очередного символа используют контексты порядка не более чем N.
Конкретные контексты, относящиеся к очередному символу из входной последовательности данных, принято называть активными контекстами.
При использовании контекстного моделирования сразу встают две проблемы
1. как выбирать оптимальный порядок контекста для оценки вероятности появления конкретного символа
2. что делать, если данный контекст еще ни разу не появлялся
С точки зрения проблемы 1 существует подразделение методов контекстного моделирования на чистые методы и смешанные. Под чистыми методами подразумевается, что используются контексты только одного порядка. Под смешанными методами подразумевается, что выполняется т.н. процесс смешивания, в котором суммарная вероятность появления символа оценивается сразу по нескольким контекстам данного символа.
Будем обозначать Pi(xi) оценку вероятности появления символа xi в позиции i входных данных. Оценку именно этой величины нам надо получить.
Простейший
алгоритм смешивания представляется следующей формулой Pi(xi)=Sl=0N w(l)P(xi|{ xi-l ,…, xi-1 })
где P(xi|{ xi-l ,…, xi-1 }) - вероятность появления символа xi в позиции i после подпоследовательности { xi-l ,…, xi-1 }, т.е. условная вероятность появления символа xi (при i=0 рассматривается просто вероятность появления символа xi , т.е. безусловная вероятность появления). w(l) представляют собой некоторые веса.
Условная вероятность вычисляется по следующей формуле
P(xi|{ xi-l ,…, xi-1 }) =
P({ xi-l ,…, xi-1 , xi }) / P({ xi-l ,…, xi-1 })=
=S({ xi-l ,…, xi-1 ,
xi })
/ S({ xi-l ,…, xi-1 })
где S({ xi-l ,…, xi-1 , xi }) –
число появлений последовательности { xi-l ,…, xi-1 , xi } во входном потоке
данных.
Приведенный алгоритм вычисления вероятностей является примером явного смешивания. Кроме этого, существует понятие неявного смешивания. При использовании контекстного моделирования с неявным смешиванием в выходной алфавит добавляется дополнительный символ – символ ухода. Для данного текущего символа xi оценка вероятности его появления вычисляется исходя из контекста максимального порядка N . Если данный контекст еще не встречался, то на выход выдается символ ухода и происходит попытка оценить вероятность появления символа исходя из модели порядка N-1. Так порядок понижается до того момента, пока не станет возможным оценить вероятность появления символа. Наличие модели 0 порядка гарантирует, что данный процесс когда-то прервется.
Отметим, что
алгоритмы контекстного сжатия можно рассматривать как обобщение, например,
адаптивного алгоритма Хаффмана, в котором вероятности появления всех символов
пересчитываются с появлением каждого нового символа. В этом случае адаптивный
алгоритм Хаффмана ничем не отличается от алгоритма контекстного сжатия порядка
0 (точнее, от соответствующей реализации данного алгоритма).
Преобразование Барроуза-Уилера (циклический сдвиг блока)
Преобразование Барроуза-Уилера само по себе не сжимает данные, но оно помогает представить их в таком виде, что степень их сжатия существующими архиваторами существенно улучшается. Отметим, что появилось оно недавно (первая ссылка – 1994г., хотя идея появилась раньше).
Пусть на входе есть некоторое слово из символов входного алфавита, например
параграф
Запишем матрицу из всех его циклических перестановок:
параграф
араграфп
раграфпа
аграфпар
графпара
рафпараг
афпарагр
фпарагра
Упорядочим строки полученной матрицы в лексикографическом порядке:
аграфпар
араграфп
афпарагр
графпара
параграф
раграфпа
рафпараг
фпарагра
Исходному слову сопоставляется код, состоящий из символов последнего столбца полученной матрицы (назовем ее Z) и номера строки в полученной матрице, в которой содержится исходное слово:
рпрафага4
Оказывается, что по полученным данным можно восстановить исходную последовательность символов.
Действительно, т.к. мы знаем все символы исходной последовательности, то отсортировав их мы получим первый столбец матрицы Z:
а……р
а……п
а……р
г……а
п……ф
р……а
р……г
ф……а
Теперь, если для каждой строки произвести циклический сдвиг вправо на одну позицию, то мы получим, что в строках матрицы Z есть слова, начинающиеся уже на пары символов: {ра, па, ра, аг, фп, аг, гр, аф}. Опять отсортировав их, мы получим уже пары символов, стоящих в первых двух столбцах матрицы Z:
аг…..р
ар…..п
аф…..р
гр…..а
па…..ф
ра…..а
ра…..г
фп…..а
И т.д. На каждом шаге мы будем получать еще один столбец матрицы Z.
В конце, когда все строки будут восстановлены, нам останется взять строку с указанным номером из полученной матрицы.
Основным достоинством данного преобразования является то, что если в исходной последовательности символов встречаются повторяющиеся слова {a0,…aN}, то соответствующие строки в матрице Z, начинающиеся на {a1,…aN} будут идти подряд, а во всех этих строках в правом столбце будет стоять один и тот же символ a0. Например, для строки папапапапа получим следующую матрицу Z:
апапапапап
апапапапап
апапапапап
апапапапап
апапапапап
папапапапа
папапапапа
папапапапа
папапапапа
папапапапа
Тогда на выходе алгоритма имеем следующий код:
пппппааааа5
Вышеописанный алгоритм неприменим на практике из-за требования большого объема памяти и вычислительных ресурсов. На самом деле можно модифицировать алгоритм так, чтобы требовалась O(N) памяти и O(N) времени на его реализацию, где N – количество символов в кодируемом блоке.
На каждом шаге описанного алгоритма мы переносим последнюю букву hi из каждой строки полученного массива i в начало строки. При этом строки были уже упорядочены, поэтому после переупорядочивания взаимное расположение строк с равным первым символом hi не изменится. Следовательно, в первой строке будет стоять строка с первым по счету минимальным hi , далее пойдет строка со вторым по счету минимальным hi (если есть несколько равных минимальных hi). Далее пойдут строки со вторым по величине hi, и т.д.
Т.о. функция t(i), сопоставляющая номеру строки i после сортировки ее номер до сортировки зависит только от последовательности { hi }. Например, для случая слова параграф имеем первый шаг алгоритма:
а……р
а……п
а……р
г……а
п……ф
р……а
р……г
ф……а
и функцию h в виде следующей таблицы:
|
i |
0 1 2 3 4 5 6 7 |
|
h(i) |
3 5 7 6 1 0 2 4 |
Исходя из полученного кода, мы знаем, что исходное слово завершается на символ ф в позиции 4. Исходя из значения функции h(4) , мы знаем, что в данную строку после сортировки перешла строка с номером h(4)=1, а значит после буквы ф должна стоять буква п (`после’ – имеется в виду – циклически). Действительно на одном шаге алгоритма кодирования мы сдвигали строку вправо и сортировали строки, а при раскодировании мы должны сделать перестановку, обратную сортировке, и применить сдвиг влево. Получим, что интересующий нас символ стоит сразу после ф в строке с номером h(4)=1. Данный процесс можно аналогично продолжить
h(4)=1
п
h(1)=5
а
h(5)=0
р
h(0)=3
а
h(3)=6
г
h(6)=2
р
h(2)=7
а
h(7)=4
ф
Итак, для всего алгоритма декодирования нам потребовалось времени = O(M+N), где M – количество символов в алфавите, N – количество символов в дешифруемом блоке. Здесь имеется в виду, что сортировку массива можно произвести за время O(M+N), и оставшуюся часть декодирования – за время O(N).
Стоит еще раз вернуться к алгоритму кодирования. Легко увидеть, что нам не нужно отводить память под матрицу циклических сдвигов исходной строки. Нам достаточно иметь массив перестановок, обеспечивающий переход от исходного массива строк с циклическими сдвигами исходной строки к отсортированному массиву. Т.е. мы можем работать с массивом целых чисел r(i), где после сортировки r(i) равно номеру исходной строки. Т.о. в процессе сортировки для сравнения i и j-той строк сортируемого массива мы будем сравнивать строки, состоящие из последовательности символов исходного массива {si,…,s(i+N)%N} и {sj,…,s(j+N)%N}.
Используя известные методы сортировки мы можем произвести сортировку за O(Nlog N) сравнений, но проблема заключается в том, что каждое сравнение требует до O(N) операций, что делает алгоритм слишком медленным в худшем случае: O(N2log N). Неприятности здесь обусловлены сравнением длинных совпадающих последовательностей символов. Поэтому требуются специальные алгоритмы сортировки. Одним из примеров таких алгоритмов является алгоритм модифицированной сортировки quick sort (алгоритм Бентли-Седжвика).
В алгоритме модифицированной сортировки используется следующая идея. В качестве медианы рассмотрим один из первых символов строк m. Разобъем массив строк на три подмассива –
1. подмассив строк, первый символ которых меньше m,
2. подмассив строк, первый символ которых больше m,
3. подмассив строк, первый символ которых равен m.
Для помассивов 1 и 2 применим тот же самый алгоритм, а для подмассива 3 применим тот же самый алгоритм, но сравнивать строки в нем будем сразу начиная со второго символа (первый символ у них совпадает).
В конце все три подмассива следует объединить в один упорядоченный массив (учитывая, что все строки из массива 1 < всех строк из массива 3 < всех строк из массива 2).
Функция, реализующая один шаг данного алгоритма будет иметь примерно следующее описание
void qsort3(char **str, int nstr, int l0, char
**tmp1, char **tmp2, char **tmp3)
{char med; int l1=0,l2=0,l3=0,i;
if(nstr<=1)return;
med=str[0][l0];//или другой алгоритм
выбора псевдо-медианы
//разбиение на 3
помассива :
for(i=0;i<nstr;i++)
if(str[i][l0]<med)tmp1[l1++]=str[i];
else
if(str[i][l0]>med)tmp2[l2++]=str[i];
else
if(str[i][l0]==med)tmp3[l3++]=str[i];
for(i=0;i<l1;i++)str[i]=tmp1[i];
for(i=0;i<l3;i++)str[i+l1]=tmp3[i];
for(i=0;i<l2;i++)str[i+l1+l3]=tmp2[i];
//рекурсия :
qsort3(str,l1,l0,tmp1,tmp2,tmp3);
qsort3(str+l1,l3,l0+1,tmp1,tmp2,tmp3);
qsort3(str+l1+l3,l2,l0,tmp1,tmp2,tmp3);
}
str – исходный массив строк длины nstr.
l0 – длина части равных префиксов строк из массива str
Используются три дополнительных массива указателей на строки длиной равной длине исходного массива строк.
Простейший пример использования данной процедуры:
int main()
{char
*str[]={"papa","r","pama","baba","ba","b"},
*tmp1[60],*tmp2[60],*tmp3[60]; int i;
qsort3(str, 6, 0, tmp1,tmp2,tmp3);
for(i=0;i<6;i++)
printf("%s\n",str[i]);
return
0;
}
Легко написать программу, имеющую меньшие требования к дополнительным массивам.
Алгоритмы сжатия изображений. Форматы представления изображений
Потоковый ввод-вывод в языке С
Понятие буферизации. Функция fflush(FILE *f);
.
Открытие файла:
FILE *fopen( const char *filename,
const char *mode );
Значения mode:
”rt”
”wt”
”at”
”rt+”
”wt+”
”rb”
”wb”
”ab”
”rb+” позволяет модифицировать файл без обрезания хвоста; если файл существует, то он не уничтожается
”wb+” позволяет модифицировать файл с обрезанием хвоста; если файл существует, то он уничтожается и создается заново
fprint, fprintf,
sprintf
scanf, fscanf,
sscanf
char *fgets( char *string,
int n, FILE *stream );
size_t fread( void *buffer,
size_t size, size_t count, FILE
*stream );
size_t fwrite( const void
*buffer, size_t size, size_t count,
FILE *stream );
//возвращают число реально прочитанных/записанных переменных
long ftell( FILE *stream
);
int fseek( FILE *stream,
long offset, int origin );
origin: SEEK_CUR, SEEK_END, SEEK_SET
fflush(FILE *f);
fclose(FILE *f);
t=текстовый режим
b=бинарный режим
По умолчанию обычно текстовый режим, но может задаваться параметром. Например, в Microsoft Visual C: глобальная переменная _fmode может принимать значения _O_TEXT или _O_BINARY, соответственно меняя режимы.
Существуют стандартные потоки stdin, stdout, stderr.
Лекция 5
Алгоритмы сжатия данных.
Список литературы
Р.Е. Кричевский. Сжатие и
поиск информации. М. Радио и связь. 1989.
Д. Ватолин, А. Ратушняк, М.
Смирнов, В. Юкин. Методы сжатия данных. М. Диалог-МИФИ. 2002.
Гюнтер Борн. Форматы данных. Киев. Торгово-издательское бюро BHV. 1995.
Алгоритмы сжатия изображений. Форматы представления изображений
Потоковый ввод-вывод в языке С
Понятие буферизации. Функция fflush(FILE *f);
.
Открытие файла:
FILE *fopen( const char *filename,
const char *mode );
Значения mode:
”rt”
”wt”
”at”
”rt+”
”wt+”
”rb”
”wb”
”ab”
”rb+” позволяет модифицировать файл без обрезания хвоста; если файл существует, то он не уничтожается
”wb+” позволяет модифицировать файл с обрезанием хвоста; если файл существует, то он уничтожается и создается заново
fprint, fprintf, sprintf
scanf, fscanf, sscanf
char *fgets(
char *string, int n, FILE
*stream );
size_t fread( void *buffer,
size_t size, size_t count, FILE
*stream );
size_t fwrite(
const void *buffer, size_t size,
size_t count, FILE *stream );
//возвращают число реально прочитанных/записанных переменных
long ftell(
FILE *stream );
int fseek( FILE *stream,
long offset, int origin );
origin:
SEEK_CUR, SEEK_END, SEEK_SET
fflush(FILE *f);
fclose(FILE *f);
t=текстовый режим
b=бинарный режим
По умолчанию обычно текстовый режим, но может задаваться параметром. Например, в Microsoft Visual C: глобальная переменная _fmode может принимать значения _O_TEXT или _O_BINARY, соответственно меняя режимы.
Существуют стандартные потоки stdin, stdout, stderr.
Замечания о представлении чисел в ЭВМ
Следует отметить, что на разных ЭВМ целые числа (short, int, long) могут иметь различные варианты представления. Тем не менее, графические файлы в стандартных форматах должны иметь одинаковый формат представления вне зависимости от типа ЭВМ. Поэтому хорошая программа чтения/записи изображений обязана уметь определять формат данных на конкретной машине и, в соответствии с этим, преобразовывать целые числа при записи на диск/чтении с диска.
Например, формат BMP подразумевает, что переменные типа short должны состоять из двух байт, старший байт слева (формат Little-Endian, в отличие от формата Big-Endian, когда слева располагается старший байт), все биты по старшинству располагаются справа налево (старший слева). Тогда функция чтения переменной unsigned short в данном формате в переменную типа unsigned long на данной ЭВМ может выглядеть следующим образом
unsigned long ReadShort(FILE *f)
{unsigned
char c[2]; fread(c,1,2,f); return c[0]+(c[1]<<8);}
Обратная функция записи может выглядеть следующим образом
int WriteShort(unsigned long i, FILE *f)
{unsigned
char c[2];
c[0]=i%256; c[1]=i/256;
return fwrite(c,1,2,f);
}
Графические изображения. Пространства цветов
Объясним, что такое графическое изображение. Прежде всего, следует отметить, что существует две основных разновидности представления графических изображений: растровые изображения и векторные изображения.
Векторные изображения задаются как набор некоторых геометрических объектов, имеющих некоторые свойства. Например, отрезки, ломаные, многоугольники, эллипсы и т.д., для которых задаются координаты вершин, цвет, толщина, стиль линии и т.д.; многоугольники, эллипсы и т.д., для которых задаются координаты вершин, цвет заполнения, стиль заполнения, параметры ограничивающей линии и т.д. Векторные изображения легко масштабировать, они имеют компактную форму представления, но графическая информация о внешнем мире, как правило, изначально не имеет векторного представления.
Растровые изображения представляются как набор пикселов, обычно, в прямоугольной матрице пикселов размером M×N, которую и называют изображением. Каждый пиксел задается своим цветом. Для представления различных цветов используются различные системы цветопередачи или пространства цветов.
Существует различные системы цветопередачи, из которых можно выделить несколько основных стандартных типов. Возможно, наиболее часто используется система цветопередачи с помощью палитры RGB, в которой пиксел задается комбинацией из трех цветов, определяющих красную, зеленую и синюю компоненты цвета. Данные вариант представления цвета согласуется с физиологией человека: на глазном дне человека находятся специфические нервные клетки: палочки и колбочки. Палочки отвечают только за яркость цвета. Существует три типа колбочек, каждый из которых ответственен за восприятие, соответственно, красного, синего и зеленого цветов.
Белый цвет (так же как и все градации серого) представляется в виде суммы равных по яркости компонент красного, синего и зеленого цветов. Для белого цвета яркость компонент должна быть максимальной, а для черного – нулевой.
Вообще, существуют и другие
варианты получения цветов смешиванием нескольких
цветов из заданного набора. Так, например, используется палитра CMY (cyan - голубой, magenta -
пурпурный, yellow - желтый). В отличие от RGB, в палитре CMY используется не сложение цветов, а вычитание
их из белого цвета. Т.о., нулевое значение компонент в палитре CMY соответствует белому цвету.
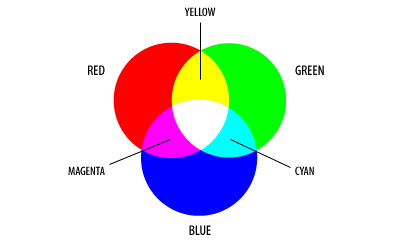
Существует простое соотношение между представлениями цвета в RGB и CMY палитрах:
RGB.r = 255-CMY.c
RGB.g = 255-CMY.m
RGB.b = 255-CMY.y
В силу своей специфики, RGB палитра широко используется в цветных мониторах, а CMY палитра используется в печати. В реальности часто вместо CMY палитры используется CMYK палитра, полученная из CMY добавлением черного цвета. Это дает возможность более точно отображать темные тона.
Способ представления цвета смешиванием стандартных цветов весьма естественен, но у него есть принципиальный недостаток: незначительные изменения отдельных компонент могут привести к существенному визуальному искажению цвета. Для устранения этого недостатка используются другие системы цветопередачи. Например, часто используется система HSV или HSB: hue – задает цвет, saturation – задает насыщенность, value (brightness) – яркость. Представим себе конус в пространстве RGB с вершиной в начале координат и осью r=g=b (ось вдоль равных значений компонент r,g,b). Угол раствора конуса задается величиной насыщенности (нулевая насыщенность соответствует серому цвету). Если спроецировать точку на конусе P на ось, то получим некоторую точку H. Тогда расстояние |OH| есть величина яркости в данной палитре. Наконец, угол между плоскостями (OHP) и (OHR), где R – точка с координатами (1,0,0) в координатах (r,g,b) задает значение цвета.
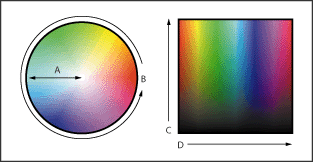
Система HSV. B=hue=цвет, A=saturation=насыщенность, C=value=яркость
В системе HLS: hue – задает цвет, saturation – задает насыщенность, lightness – яркость. hue=0 соответствует синему цвету, hu=60° соответствует пурпурному цвету, hue=120° соответствует красному цвету.
Форматы BMP и RLE
Формат BMP исторически
является основным форматом представления изображений в ОС Microsoft Windows*. Постараемся
дать, по возможности, полное описание формата.
Обычно формат не использует алгоритмов сжатия.
Поэтому не представляет особого труда написать собственную программу,
позволяющую считывать изображения с диска (т.е. конвертировать их из BMP формата в формат,
удобный для непосредственного использования) и записывать их на диск.
Данный формат дает возможность представлять изображения с палитрой или без нее. При наличии палитры значение цвета в каждом пикселе задается номером цвета. Сам цвет определяется по его номеру в палитре, представляющей собой массив
unsigned char pal[256][4];
Каждая строка в массиве палитры задает один цвет с помощью указания его RGB составляющих, соответственно, в ячейках с номерами 0, 1, 2. Количество строк зависит от количества используемых цветов и, обычно, не превосходит 256 (что соответствует изображению, в котором на один пиксел отводится 8 бит).
Данные можно представлять в формате true color, когда каждый пиксел задается 4-мя байтами. Из них используется 3 байта для размещения RGB компонент цвета (по одному байту на каждую компоненту).
Возможно большое количество нестандартных вариаций данного формата. Например, отсутствие палитры в изображениях с толщиной 8 бит на пиксел может обозначать, что кодируется серое изображение, в каждом байте которого хранится яркость пиксела. Некоторые программы понимают форматы BMP в которых отводится 3 байта на пиксел (формат true color) или даже 2 байта на пиксел (в пикселе хранится только яркость, т.е. кодируется серое изображение).
Файл состоит из следующих разделов:
· Заголовка
· Возможно – палитры
· Собственно данных
Заголовок файла представляется следующей структурой
struct
BMPHEAD
{
unsigned short int Signature
; //
Must be 0x4d42 == ”BM” //0
unsigned long FileLength
; // в байтах //2
unsigned long Zero ; //
Must be 0 //6
unsigned long Ptr ; // смещение к области данных //10
unsigned long Version ;// длина оставшейся части
заголовка=0x28 //14
unsigned long Width ;
// ширина изображения в
пикселах //18
unsigned long Height ; //
высота изображения в пикселах //22
unsigned short int
Planes ; //
к-во битовых плоскостей //26
unsigned short int
BitsPerPixel ; // к-во
бит на папиксел //28
unsigned long Compression ; // сжатие: 0 или 1 или 2 //30
unsigned long SizeImage ; // размер блока данных в байтах //34
unsigned long XPelsPerMeter ; // в ширину: пикселов на метр //38
unsigned long YPelsPerMeter ; // в высчоту: пикселов на метр //42
unsigned long ClrUsed ; // к-во цветов в палитре //46
unsigned long ClrImportant ; // к-во используемых
цветов в палитре //50
} ;
Предполагается, что sizeof(unsigned long)==4, sizeof(unsigned short
int)==2.
Соответствующие поля в файле с данным форматом непрерывно располагаются в указанном порядке.
Палитра (если она есть) следует сразу за заголовком. Данные начинаются с байта номер Ptr, начиная от начала файла.
BMP без сжатия.
Поле Compression определяет способ сжатия данных. Обычно значение этого поля=0, что соответствует отсутствию сжатия. При этом данные записываются по битам подряд. BMP формат со сжатием часто называется RLE форматом.
Длина каждой строки округляется в большую сторону до кратности 32 битам (4 байта). Т.о., например, при отсутствии сжатия если Width=3, то каждая строка на диске будет занимать
(Width* BitsPerPixel + 31)/8=4 байт.
Предполагается, что байты располагаются в порядке их нумерации, старший бит слева. Т.о., если BitsPerPixel =1, то самый первый пиксел ляжет в старший бит самого первого байта данных.
Для хранения всего изображения структуру struct BMPHEAD следует дополнить массивом палитры и массивом самих данных. Если предположить, что мы будем иметь дело с изображениями не более 8 бит на пиксел, то для данных можно завести, например, массив unsigned char **v . Пиксел с координатами (i,j) можно хранить в переменной v[i][j].
Итак, все изображение можно хранить в структуре
struct CBMP
{
unsigned short int Signature
; //
Must be 0x4d42 == ”BM” //0
unsigned long FileLength
; // в байтах //2
unsigned long Zero ; //
Must be 0 //6
unsigned long Ptr ; // смещение к области данных //10
unsigned long Version ;// длина оставшейся части
заголовка=0x28 //14
unsigned long Width ;
// ширина изображения в
пикселах //18
unsigned long Height ; //
высота изображения в пикселах //22
unsigned short int
Planes ; //
к-во битовых плоскостей //26
unsigned short int
BitsPerPixel ; // к-во
бит на папиксел //28
unsigned long Compression ; // сжатие: 0 или 1 или 2 //30
unsigned long SizeImage ; // размер блока данных в байтах //34
unsigned long XPelsPerMeter ; // в ширину: пикселов на метр //38
unsigned long YPelsPerMeter ; // в высчоту: пикселов на метр //42
unsigned long ClrUsed ; // к-во цветов в палитре //46
unsigned long ClrImportant ; // к-во используемых
цветов в палитре //50
unsigned char pal[256][4];
unsigned char **v;
} ;
Отвести память можно, например, следующим образом:
struct CBMP pic; int i;
…
pic.v=(unsigned
char**)malloc(pic.Height*sizeof(char*));
for(i=0;i<pic.Height;i++)pic.v[i]= (unsigned
char*)malloc(pic.Width);
Однако следующий способ гораздо более эффективен:
struct CBMP pic; int i;
…
pic.v=(unsigned
char**)malloc(pic.Height*sizeof(char*)+pic.Height*pic.Width);
pic.v[0]= (unsigned char**)(pic.v+pic.Height);
for(i=1;i<pic.Height;i++)pic.v[i]=pic.v[i-1]+pic.Width;
Преимуществом такого способа отведения памяти является уменьшение накладных расходов и упрощение процедуры освобождения памяти. Для освобождения отведенной памяти надо вызвать всего один оператор:
free(pic.v);
BMP со сжатием.
Значение поля Compression=1 соответствует RLE-сжатию для изображений, имеющих 8 бит на пиксел. Значение поля Compression=2 соответствует RLE-сжатию для изображений, имеющих 4 бит на пиксел.
Опишем RLE-сжатие для случая 8 бит на пиксел. В этом случае строка данных представляется записями одного из двух форматов.
Формат 1:
повторитель,
цвет
Т.е. если есть набор подряд идущих пикселов с одинаковыми значениями то их можно закодировать указанным способом, отведя по одному байту на повторитель и одному байту на цвет. Счетчик может принимать значения от 1 до 255.
Формат 2:
0x00, счетчик, данные
Т.е. в этом случае сначала выводится байт с нулевым значением, далее следует байт со значением N от 3 до 0xff, далее следует последовательность данных длиной N байт. Значения счетчика от 0 до 2 имеют следующий смысл:
0 конец строки (т.е. в подобном изображении могут быть области с неопределенным цветом, что удобно для изображений нестандартной форы)
1 конец изображения
2 delta record. В этом случае после счетчика следуют два байта со значениями x, y, указывающими относительное смещение текущей точки. Т.о. формат позволяет перепрыгивать от описания одного блока изображения к описанию другого блока.
Формат PCX
Формат также довольно прост. Заголовок имеет следующий вид
struct SPCXHEAD
{
unsigned char manuf; //=10
для PaintBrush
unsigned char hard; //
версия
unsigned char encod; // Групповое
кодирование =1
unsigned char BitsPerPixel; // Бит на точку в одной плоскости
short int x1; // Размеры картинки
short int y1;
short int x2;
short int y2;
short int hres; // Гориз.разрешение дисплея
short int vres; // Верт.разрешение дисплея
unsigned char pal[48]; // Палитра
unsigned char vmode; //
unsigned char
nplanes; // Кол-во плоскостей
short int bplin; //
Байт на строку (для одной плоскости)
short int palinfo; //
Инф о палитре (1=цв.;2=сер.)
short int shres; // Разрешение
short int svres;
char xtra[54]; // Доп.пустое место (фильтр)
}; //
Размер = 81 байт
В отличие от BMP-формата данный формат всегда использует сжатие, хотя эффективным оно бывает редко.
Если количество цветов не превосходит 16 (4 бит на пиксел), то палитра умещается в заголовке, иначе она дописывается после данных.
Данные для каждой отдельной строки записываются по битовым плоскостям. Сначала – все биты строки из первой плоскости, потом – все биты второй и т.д. Сжатие производится с помощью повторителей: в повторителе первые два бита равны 1 и служат признаком повторителя. Т.е. если требуется записать некоторый байт x с повторителем n<64, то на выход подаются 2 байта:
n|(128|64)
x
Если на выход требуется подать один байт со значением x<0xC0=(1100 0000)2 , то байт подается без изменений, иначе на выход подается повторитель и байт x:
1|(128|64)
= 193 = 0xC1
x
Алгоритм распаковки очевиден.
Формат GIF
GIF = Graphics Interchange Format. Формат оптимизирован для передачи изображения по сети. Для того, чтобы иметь возможность быстрого просмотра изображения, строки изображения могут передаваться не последовательно, а с шагом в 8 строк. Т.о., изображение передается за 8 этапов, каждый из которых улучшает качество уже переданного изображения. Строки передаются в следующем порядке начальных строк: 4, 2, 1, 3, 5, 7.
Данные сжимаются некоторой версией алгоритма LZW.
В одном файле может храниться несколько изображений.
Формат TIFF
TIFF = Tag Image File Format.
Очень сложный формат, поддерживающий потенциальную возможность использования произвольных форм хранения растровых изображений.
Файл состоит из заголовка, однонаправленного списка блоков записей и данных, расположенных между блоками записей.
Заголовок состоит всего из трех полей:
· 2 байта идентификатора формата (”I I” = формат Intel представления целых чисел, т.е. младший байт располагается раньше; ”M M” = формат Motorola представления целых чисел, т.е. старший байт располагается раньше)
· 2 байта с номером версии
· 4 байта с индексом первого блока записей
Блок записей (Image File Directory) состоит из поля с количеством записей N (2 байта), далее следуют N записей (tags) (каждая по 12 байт), далее следует 4-х-байтный указатель на следующий блок записей (=смещение от начала файла; нулевое значение информирует о последнем блоке записей).
Каждая запись (tag) состоит из четырех полей
· тип tag (2 байта)
· тип данных (2 байта)
· длина поля данных (4 байта)
· значение данных или указатель на поле данных (4 байта)
Существует много различных типов записей (типов tags). Для каждой новой версии TIFF формата могут добавляться новые типы записей.
Типов данных всего 4:
1. байтовый
2. ASCII
3. 16-битное целое
4. 32-битное
целое
5. дробь: 2 байта числитель, 2 байта знаменатель.
Длина поля данных указывается в терминах соответствующего типа, т.е. при значении типа данных = 4, длине поля данных = 10, получим, что поле данных занимает 40 байт.
Например, ширина изображения N помещается в запись со следующими полями:
·
0x100 (=тип соответствующей записи)
·
3 (=формат есть 2-байтовое целое)
· 1 (=длине поля данных, т.е. все поле помещается в следующих 4 байтах)
· N
Для сжатия графических данных используются различные алгоритмы. Например, для сжатия 2-цветных изображений используются два основных алгоритма. Это – PackBit и фиксированный код Хаффмана. Также используется алгоритм LZW.
Алгоритм PackBit кодирует байты каждой строки изображения в следующем формате:
Счетчик, последовательность байт.
Счетчик занимает 1 байт. Для значения счетчика от 0 до 0x7F далее следует указанное в счетчике количество байт без сжатия. Для значений счетчика X от 0x81 до 0xFF далее следует всего один байт, который при раскодировании повторяется X-0x80 раз.
Фиксированный код Хаффмана используется для кодирования длин последовательностей белых и черных пикселов в строках изображения. Предполагается, что строка начинается с последовательности белых пикселов (если строка начинается с черного пиксела, то длина первой последовательности белых пикселов кладется равной 0).
Для кодирования длин последовательностей одинаковых бит используются различные коды для белых и черных пикселов. Для пикселов одного цвета существует два типа кодов: коды восстановления и коды завершения. Длина каждой последовательности кодируется некоторым количеством кодов восстановления и далее одним кодом завершения. Для длин менее 64 используется только один код завершения.
Лекция 6
Алгоритмы сжатия данных.
Список литературы
Р.Е. Кричевский. Сжатие и
поиск информации. М. Радио и связь. 1989.
Д. Ватолин, А. Ратушняк, М.
Смирнов, В. Юкин. Методы сжатия данных. М. Диалог-МИФИ. 2002.
Гюнтер Борн. Форматы данных. Киев. Торгово-издательское бюро BHV. 1995.
Алгоритмы сжатия изображений. Форматы представления изображений
Формат PCX
Формат также довольно прост. Заголовок имеет следующий вид
struct SPCXHEAD
{
unsigned char manuf; //=10
для PaintBrush
unsigned char hard; //
версия
unsigned char encod; // Групповое
кодирование =1
unsigned char BitsPerPixel; // Бит на точку в одной плоскости
short int x1; // Размеры картинки
short int y1;
short int x2;
short int y2;
short int hres; // Гориз.разрешение дисплея
short int vres; // Верт.разрешение дисплея
unsigned char pal[48]; // Палитра
unsigned char vmode; //
unsigned char
nplanes; // Кол-во плоскостей
short int bplin; // Байт на строку (для одной плоскости)
short int palinfo; //
Инф о палитре (1=цв.;2=сер.)
short int shres; // Разрешение
short int svres;
char xtra[54]; // Доп.пустое место (фильтр)
}; //
Размер = 81 байт
В отличие от BMP-формата данный формат всегда использует сжатие, хотя эффективным оно бывает редко.
Если количество цветов не превосходит 16 (4 бит на пиксел), то палитра умещается в заголовке, иначе она дописывается после данных.
Данные для каждой отдельной строки записываются по битовым плоскостям. Сначала – все биты строки из первой плоскости, потом – все биты второй и т.д. Сжатие производится с помощью повторителей: в повторителе первые два бита равны 1 и служат признаком повторителя. Т.е. если требуется записать некоторый байт x с повторителем n<64, то на выход подаются 2 байта:
n|(128|64)
x
Если на выход требуется подать один байт со значением x<0xC0=(1100 0000)2 , то байт подается без изменений, иначе на выход подается повторитель и байт x:
1|(128|64)
= 193 = 0xC1
x
Алгоритм распаковки очевиден.
Формат GIF
GIF = Graphics Interchange Format. Формат оптимизирован для передачи изображения по сети. Для того, чтобы иметь возможность быстрого просмотра изображения, строки изображения могут передаваться не последовательно, а с шагом в 8 строк. Т.о., изображение передается за 8 этапов, каждый из которых улучшает качество уже переданного изображения. Строки передаются в следующем порядке начальных строк: 4, 2, 1, 3, 5, 7.
Данные сжимаются некоторой версией алгоритма LZW.
В одном файле может храниться несколько изображений.
Формат TIFF
TIFF = Tag Image File Format.
Очень сложный формат, поддерживающий потенциальную возможность использования произвольных форм хранения растровых изображений.
Файл состоит из заголовка, однонаправленного списка блоков записей и данных, расположенных между блоками записей.
Заголовок состоит всего из трех полей:
· 2 байта идентификатора формата (”I I” = формат Intel представления целых чисел, т.е. младший байт располагается раньше; ”M M” = формат Motorola представления целых чисел, т.е. старший байт располагается раньше)
· 2 байта с номером версии
· 4 байта с индексом первого блока записей
Блок записей (Image File Directory) состоит из поля с количеством записей N (2 байта), далее следуют N записей (tags) (каждая по 12 байт), далее следует 4-х-байтный указатель на следующий блок записей (=смещение от начала файла; нулевое значение информирует о последнем блоке записей).
Каждая запись (tag) состоит из четырех полей
· тип tag (2 байта)
· тип данных (2 байта)
· длина поля данных (4 байта)
· значение данных или указатель на поле данных (4 байта)
Существует много различных типов записей (типов tags). Для каждой новой версии TIFF формата могут добавляться новые типы записей.
Типов данных всего 5:
6. байтовый
7. ASCII
8. 16-битное целое
9. 32-битное
целое
10. дробь: 2 байта числитель, 2 байта знаменатель.
Длина поля данных указывается в терминах соответствующего типа, т.е. при значении типа данных = 4, длине поля данных = 10, получим, что поле данных занимает 40 байт.
Например, ширина изображения N помещается в запись со следующими полями:
·
0x100 (=тип соответствующей записи)
·
3 (=формат есть 2-байтовое целое)
· 1 (=длине поля данных, т.е. все поле помещается в следующих 4 байтах)
· N
Для сжатия графических данных используются различные алгоритмы. Например, для сжатия 2-цветных изображений используются два основных алгоритма. Это – PackBit и фиксированный код Хаффмана. Также используется алгоритм LZW.
Алгоритм PackBit кодирует байты каждой строки изображения в следующем формате:
Счетчик, последовательность байт.
Счетчик занимает 1 байт. Для значения счетчика от 0 до 0x7F далее следует указанное в счетчике количество байт без сжатия. Для значений счетчика X от 0x81 до 0xFF далее следует всего один байт, который при раскодировании повторяется X-0x80 раз.
Фиксированный код Хаффмана используется для кодирования длин последовательностей белых и черных пикселов в строках изображения. Предполагается, что строка начинается с последовательности белых пикселов (если строка начинается с черного пиксела, то длина первой последовательности белых пикселов кладется равной 0).
Для кодирования длин последовательностей одинаковых бит используются различные коды для белых и черных пикселов. Для пикселов одного цвета существует два типа кодов: коды восстановления и коды завершения. Длина каждой последовательности кодируется некоторым количеством кодов восстановления и далее одним кодом завершения. Для длин менее 64 используется только один код завершения.
Алгоритмы сжатия изображений с потерями. Форматы представления изображений
В случае работы с изображениями мы можем себе позволить при сжатии терять некоторую, визуально слабо заметную, часть изображения. Существует целый ряд алгоритмов сжатия с потерями.
Стандартной проблемой сжатия с потерями является отсутствие четкого критерия `похожести’ двух изображений. Среднеквадратичная оценка близости (mean squared error (MSE)) плоха в силу очевидных обстоятельств: если понизить яркость всего изображения на 5%, то заметить это будет крайне сложно, а если внести в изображение такой же белый шум, то разница между исходным и модифицированным изображением будет очевидна. Поэтому для оценки разности двух изображений лучше использовать не только l2 -норму разности изображений, но и норму разностной производной разности изображений. Например, для изображений X и Y размером M´N:
r(X,Y)2 = aSij (xij – yij)2 / ( M2N2 ) +
+ bSij ( ((xij
– yij)- (xij-1 –
yij-1))2 + ((xij – yij)- (xi-1j – yi-1j))2
) /
( M2N2 )
здесь a,b - некоторые неотрицательные веса.
Имеет, также, смысл тот факт, что
визуальная оценка разности двух изображений имеет явно не линейный характер.
Поэтому в простейшем случае чаще используют не среднеквадратичную разность
изображений, а оценку, основанную на логарифме этой величины. Так вводится
понятие отношение сигнала к шуму (PSNR : peak-to-peak signal-to-noise ratio):
PSNR=10 log10 ( ( M2N2 H2) / Sij (xij – yij)2)
здесь H – максимальное значение яркости изображения (часто H=255).
Совпадающие изображения имеют PSNR, равный плюс бесконечности. Максимально отличающиеся изображения (полностью белое и полностью черное) имеют PSNR=0. Считается, что сильно похожие изображения имеют PSNR= 40-43, а изображения, имеющие PSNR<30 , имеют явное различие.
Формат JPEG
Данный формат является наиболее стандартным из форматов изображений, обеспечивающих их сжатие с потерями. Сжатие происходит в результате нескольких преобразований.
1. RGB -> YUV. Первое, что происходит это – смена представления цвета. Представление цвета в палитре RGB заменяется на представление YUV. В представлении YUV компонента Y отвечает за яркость, а компоненты U и V, соответственно, за красную и синюю компоненты цвета. Формулы преобразования:
YUV.Y = [0.299*RGB.R + 0.587*RGB.G + 0.114*RGB.B] ;
YUV.U = [RGB.R - YUV.Y]/2 +128 ;
YUV.V := RGB.B - YUV.Y]/2 +128 ;
Отметим, что цвет в формате YUV также используется в европейском телевизионном стандарте PAL .
Оказывается, что после этого преобразования можно сразу сократить количество бит на представление компонент U и V, т.к. человеческий глаз менее чувствителен к изменению цвета, чем к изменению яркости.
2. Разбиение на квадраты 8´8. При большей степени сжатия для компонент U и V используются строки и столбцы матрицы изображения через 1, а для компоненты Y все остается по старому. Поэтому общий объем данных сокращается сразу вдвое.
3. Далее используется дискретное косинусное преобразование данных в каждом квадрате.
Под этим имеется в виду
следующее. Рассмотрим сначала одномерный случай. Если на [0,1] рассмотреть
скалярное произведение функций в L2, то в нем функции ji(x)=cos(pix) окажутся
ортогональными. Действительно при j¹ i:
(ji, jj) = ò01 cos(pix) cos(pjx) dx=ò01 (cos(p(i+j)x)+ cos(p(j-i)x))/2 dx=
=ò01 cos(p(i+j)x) /2 dx + ò01 cos(p(j-i)x)/2 dx=0+0=0
Оказывается, что аналогичный факт верен и в дискретном случае. Рассмотрим функции v(i): N->R. Пусть i принимает значения от 0 до N-1. На множестве этих функций, называемых сеточными функциями, зададим скалярное произведение:
(u,v) = Si=0N ui vi /N
Оказывается, что функции
j
i (x)= cos(p(2x+1)j/(2N))
будут ортогональными в этом скалярном произведении.
Действительно, при i¹j:
N (j i, j j) = Sx=0N-1 cos(p(2x+1)j/(2N)) cos(p(2x+1)i/(2N)) =
=Sx=0N-1 cos(p(i+j) (2x+1)/(2N)) /2 + cos(p(j-i) (2x+1)/(2N))/2=
=Sx=0N-1Re(cos(p(i+j) (2x+1)/(2N)) /2 + i sin(p(i+j) (2x+1)/(2N)) /2 +
+cos(p(j-i) (2x+1)/(2N))/2) +i sin
(p(j-i) (2x+1)/(2N))/2))=
=Re(Sx=0N-1exp(i p(i+j) (2x+1)/(2N)) + Sx=0N-1exp(i p(i-j) (2x+1)/(2N)) )/2=
=Re(exp(i p(i+j)/(2N))Sx=0N-1exp(i p(i+j) x/N) +
exp(i p(i-j)/(2N))Sx=0N-1exp(i p(i-j) x/N) )/2=
=Re(exp(i p(i+j)/(2N)) (1-exp(i p(i+j) ))/(1- exp(i p(i+j)/N)) +
exp(i p(i-j)/(2N))(1-exp(i p(i-j) ))/( 1- exp(i p(i-j)/N)) )/2=
=Re((1-exp(i p(i+j) ))/( exp(-i p(i+j)/(2N))- exp(i p(i+j)/(2N))) +
(1-exp(i p(i-j) ))/( exp(-i p(i-j)/(2N))- exp(i p(i-j)/(2N))) )/2=
=Re((1-exp(i p(i+j) ))/( -2 i sin(p(i+j)/(2N))) +
(1-exp(i p(i-j) ))/(-2 i sin (p(i-j)/(2N))) )/2=
=Re((1±1)/( -2 i sin (p(i+j)/(2N))) +
(1-±1)/(-2 i sin (p(i-j)/(2N))) )/2=0
При i=j¹0 в данной формуле получится деление на 0.
(j i, j i) =1/N Sx=0N-1 cos(p(2x+1)i/(2N)) cos(p(2x+1)i/(2N)) =
=1/N Sx=0N-1 cos(p i (2x+1)/N) /2 + cos(p 0 (2x+1)/(2N))/2=
=0+N/2/N=1/2
При i=j=0 :
(j i, j i) =1/N Sx=0N-1 cos(p(2x+1)i/(2N)) cos(p(2x+1)i/(2N)) =
=1/N Sx=0N-1 cos(p i (2x+1)/N) /2 + cos(p 0 (2x+1)/(2N))/2=
=0+N/2/N=1
Т.е. функции j j являются ортогональными, а функции y j=j j /sqrt(j j , j j) являются ортонормированными.
Итак, получаем, что для разложения функции u по функциям j i (x)= cos(p(2x+1)j/(2N)) :
u(x)= Sk=0N-1 ck j k (x)
коэффициенты разложения ck ищутся по формуле
ck = (u, j k )/ (j k , j k ) =Ak Sx=0N-1 u(x) cos(p(2x+1)k/(2N)),
где A=(2, если k>0; 1, если k==0)
Коэффициенты ck называются cos-преобразованием исходной функции u.
Для двумерного изображения данное преобразование производится по двум направлениям:
ckl
=Akl S u(x,y) cos(p(2x+1)k/(2N)) cos(p(2y+1)l/(2M))
4. Далее в полученной матрице, в зависимости от степени сжатия, обнуляются несущественные элементы.
5. Матрица 8´8 переводится в вектор, зигзагообразным обходом:
{a00, a10, a01,
a20, a11, a02, a30, a21,
a12, a03, …} = {b0, b1, b2, b3, …}
т.о. самые существенные коэффициенты (отвечающие за гладкую составляющую изображения) оказываются в начале вектора.
6. Полученный вектор b кодируется парами чисел вида
{сколько_чисел_пропустить, очередное_число}.
Например последовательность {10, 11, 0, 0, 12, 13,0,0,1,…} кодируется:
{0,10, 0,11, 2,12, 0,13, 2,1, …}
7. Полученный вектор кодируется фиксированным кодом Хаффмана.
Wavelet – сжатие. Алгоритм JPEG-2000
Данный подход использует ту же идею, что и в случае JPEG-сжатия. Отличием является выбор другого набора базисных функций. Основным недостатком cos-преобразования является то, что все рассматриваемые базисные функции имеет нелокализованный носитель. Это приводит к тому, что резкие перепады в одной части изображения сказываются на всех коэффициентах разложения.
В случае Wavelet-сжатия также используются некоторый ортогональный базис. Но, в отличие от JPEG-сжатия, существенная часть функций здесь имеет локализованный носитель.
Будем рассматривать лишь дискретный случай. Опустим строгое определение вейвлетов. Рассмотрим лишь, собственно, алгоритм.
В основе любого вейвлета лежит два фильтра: H0 и H1 , первый из которых обязан, в каком-то смысле, сглаживать исходную функцию, а второй совершать, в некотором смысле, обратное преобразование. Под фильтром H подразумевается процедура свертки с некоторой функцией h:
H0(u) = u*h
H0(u)( i ) = S u(i-j) h(i)
Самыми простыми вейвлетами
являются вейвлеты Хаара. Для них
H0(u) ( i ) = u(i)*0.5 + u(i-1)*0.5 (h(0)=0.5, h(1)=0.5)
H1(u) ( i ) = u(i)*0.5 - u(i-1)*0.5 (h(0)=0.5, h(1)=-0.5)
Вейвлет-преобразование W(u) заключается в том, что мы применяем к исходной функции u фильтр H0 и берем каждое второе полученное значение. Результат даст нам первую половину вектора результата v . Далее мы применяем к исходной функции u фильтр H1 и опять берем каждое второе полученное значение. Результат даст нам вторую половину вектора результата v .
Итого в первой половине вектора v будут лежать коэффициенты, отражающие гладкую составляющую вектора u, а во торой половине – не гладкую.
Далее для первой половины вектора
v мы
повторим ту же процедуру и результат поместим опять в первую половину вектора v. Далее повторим процедуру
для первой четверти вектора v . И т.д. [log2 N] раз, где N – размер вектора u.
Т.о. в начальной части вектора v будут собираться компоненты, отвечающие за его гладкую часть, а в конце останутся компоненты, отвечающие за не гладкую часть.
Данную процедуру легко обобщить на 2-мерный случай. В алгоритме JPEG-2000 вместо cos-преобразования используется 2-мерное вейвлет – преобразование Хаара, а вместо сжатия Хаффмана – арифметическое сжатие.
Двумерное вейвлет – преобразование Хаара представляет собой следующее. Изображение разбивается на 4 части
B00 B01
B10 B11
Фильтры представляют собой следующее
H00(u)( i ) = (u(i,j) + u(i-1,j) + u(i,j-1) + u(i-1,j-1))/4
H10(u)( i ) = (u(i,j) - u(i-1,j) + u(i,j-1) - u(i-1,j-1))/4
H01(u)( i ) = (u(i,j) + u(i-1,j) - u(i,j-1) - u(i-1,j-1))/4
H11(u)( i ) = (u(i,j) - u(i-1,j) - u(i,j-1) + u(i-1,j-1))/4
Соответственно, после применения каждого фильтра оставляются каждый второй столбец и каждая вторая строка матрицы. Результат применения фильтра Hij помещается в блок Bij.
Далее аналогичная процедура производится для блока B00.
И т.д.
Если получившуюся матрицу обозначить cij , то в c00 будет в конечном счете лежать среднее значение всего изображения. В c10 будет располагаться разность средних значений в исходных блоках B00 и B10 . В c01 будет располагаться разность средних значений в исходных блоках B00 и B01 . И т.д.
Фрактальное сжатие
Фрактальное сжатие, практически не имеет конкурентов по качеству сжатия для довольно широкого класса изображений, но его использование сдерживается медленной скоростью реализации данного алгоритма. Существуют многочисленные работы, призванные ускорить данный алгоритм.
Фрактальными множествами называются множества, обладающие следующими свойствами:
1. Самоподобие
2. Хаусдорфова размерность множества не целая
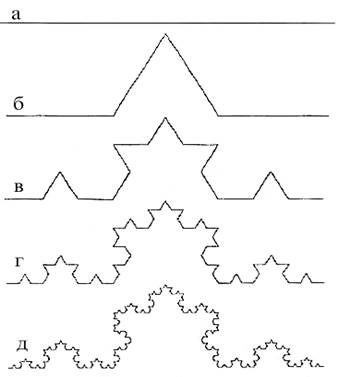
Рисунок 1. Этапы построения снежинки
Коха
Под самоподобием понимается следующий факт: для любой части объекта найдется ее меньшая часть, в каком-то смысле подобная данной.
Хаусдорфовой или фрактальной размерностью объекта XÌ Rn называется r, определяемой следующим образом. Разобьем все пространство Rn на кубы со стороной h , вершины которых лежат в точках сетки (i1h, i2h, …, inh). Пусть Kh - объединение кубов с шагом h, имеющих непустое пересечение с X. Тогда определим
r=lim h®0 log |Kh| / log h (если такой предел существует)
Например, на плоскости для отрезка [(0,0), (0,1)] имеем:
|Kh|= 2 é1/hù h2=2h(1+o(1))
log |Kh| / log h= log (2h(1+o(1))) / log h=1+ log (2(1+o(1))) / log h
lim h®0 log |Kh| / log h=1
Оказывается, что подавляющее большинство природных объектов обладают свойством фрактальности. С другой стороны, объекты созданные человеком, редко обладают этим свойством. Фрактальное сжатие активно использует свойство самоподобия изображений. При этом оказывается, что изображения природных объектов (например, изображение леса) поддаются фрактальному сжатию существенно лучше, чем, например, городской ландшафт.
Основная идея фрактального сжатия заключается в следующем. Рассмотрим для простоты серое изображение. График изображения, как график функции двух переменных, является объектом трехмерного пространства. Попробуем найти сжимающее отображение, переводящее данный график в себя. Вместо функции будет хранить некоторое описание этого сжимающего отображения.
Естественно, что таких отображений существует много. Мы будем искать отображение среди отображений в некотором классе. При этом оказывается, что такого отображения может вообще не существовать и мы будем искать отображение, переводящие изображение в некоторое близкое к нему. Исходя из свойств отображения, мы сможем получить оценку на норму разности исходного изображения и неподвижной точки найденного сжимающего отображения через норму разности исходного отображения и его образа после применения к нему найденного отображения.
Рассматривается следующий класс сжимающих отображений. Изображение разбивается на квадраты со стороной m. Назовем данные квадраты малыми. Вместе с тем, изображение разбивается на квадраты со стороной 2m. Назовем такие квадраты большими. В рассматриваемом классе отображений график функции на каждом малом квадрате ti получается в результате некоторого аффинного преобразования Li из графика функции на некотором большом квадрате Ti .Естественно, что при этом аффинное преобразование Li имеем вид
é a b 0ù
é xù é fù
Li (x,y,z)= ê c d 0 ê
ê y
ê
+ ê g ê
ë 0 0 e û ë z û ë hû
a b
Матрица c d задает аффинное преобразование, отображающее большой квадрат в малый. Легко увидеть, что таких отображение всего 8. Остается одномерное преобразование ez+h , перемещающее график изображения по оси Z. Это отображение задается двумя коэффициентами e, z. Условие сжимаемости: z<1.
Итак, для изображения размером M´N для каждого малого квадрата для задания отображения следует выделить 3 бита для преобразования квадрата, log2M+log2N бит для задания номера большого квадрата, две ячейки для задания коэффициентов e, z.
Алгоритм поиска оптимального сжимающего отображения для каждого малого квадрата сводится к следующему. Необходимо перебрать все большие квадраты. Для каждого из них надо перебрать все 8 вариантов отображений квадратов. Для каждого из отображений следует вычислить оптимальные e, z. В результате, после вычисления образа полученного отображения, мы имеем норму разности полученного изображения и исходного на малом квадрате - e.
Изо всех вышеописанных вариантов надо выбрать вариант с минимальной величиной e. Данный вариант и будет отображением в рассматриваемый малый квадрат.
Осталось описать алгоритм вычисления e, z. Сначала функция с большого квадрата u проецируется на малый. Это можно сделать, например, осредняя значение функции в каждых четырех соседних точках. Задача свелась к минимизации по e, z следующего выражения
S (euij+z-vij)2 = e2S uij2 +ez 2S uij-e2S uijvij+z2m2-z2S vij +S vij2
Беря частные производные по e и z, получим систему уравнений 2´2:
e 2S uij2 +z 2S uij=2S uijvij
e 2S uij +z2m2 =2S vij
Итого, у нас есть всего M/m N/m малых квадратов и M/2/m N/2/m больших. Для каждого малого квадрата и для каждого большого надо перебрать 8 вариантов отображений и для каждого время вычисления оптимального отображения есть O(m2). Т.о. суммарное время работы алгоритма
T(M,N,m) = O(M2N2/m2)
Существуют различные способы ускорения алгоритма. Основным из них – введения понятие индекса квадрата. Индексом называется разбиение множества всевозможных функций на квадрате на классы эквивалентности такие, что удачное сжимающее отображение может существовать только в случае, когда образ и прообраз отображения лежат в одном классе эквивалентности. Тогда для каждого малого квадрата поиск ведется только среди больших квадратов своего класса эквивалентности.
Существуют алгоритмы, когда малые квадраты имеют непостоянный размер. Т.е. если для данного размера малого квадрата не удалось найти удачного большого квадрата, то малый квадрат может разбиваться на подквадраты и для них будет применен тот же алгоритм поиска.
Шпаргалка для контрольной работы
struct
BMPHEAD
{
unsigned short int Signature
; //
Must be 0x4d42 == ”BM” //0
unsigned long FileLength
; // в байтах //2
unsigned long Zero ; //
Must be 0 //6
unsigned long Ptr ; // смещение к области данных //10
unsigned long Version ;// длина оставшейся части
заголовка=0x28 //14
unsigned long Width ;
// ширина изображения в
пикселах //18
unsigned long Height ; //
высота изображения в пикселах //22
unsigned short int
Planes ; //
к-во битовых плоскостей //26
unsigned short int
BitsPerPixel ; // к-во
бит на папиксел //28
unsigned long Compression ; // сжатие: 0 или 1 или 2 //30
unsigned long SizeImage ; // размер блока данных в байтах //34
unsigned long XPelsPerMeter ; // в ширину: пикселов на метр //38
unsigned long YPelsPerMeter ; // в высчоту: пикселов на метр //42
unsigned long ClrUsed ; // к-во цветов в палитре //46
unsigned long ClrImportant ; // к-во используемых
цветов в палитре //50
} ;
FILE *fopen( const char *filename,
”rb+”);
size_t fread( void *buffer,
size_t size, size_t count, FILE
*stream );
fflush(FILE *f);
size_t fwrite( const void *buffer,
size_t size, size_t count, FILE
*stream );
long ftell( FILE *stream
);
int fseek( FILE *stream,
long offset, int origin );
origin:
SEEK_CUR, SEEK_END, SEEK_SET
fclose(f);
Пример задачи для контрольной работы.
Известно, что обрабатываемый BMP-файл имеет 8 бит на пиксел и то, что он задается в серой
палитре (т.е. значение пиксела задает яркость). Требуется нарисовать в данном
изображении черный крест с центром в позиции (i,j). Имя BMP-файла и
значения i, j задаются в виде параметров
программы. Пример вызова программы:
./prog pic.bmp 10 10
При работе следует модифицировать существующий файл, т.е. открывать его
на чтение с модификацией.
Лекция 7
Алгоритмы сжатия данных.
Список литературы
Р.Е. Кричевский. Сжатие и
поиск информации. М. Радио и связь. 1989.
Д. Ватолин, А. Ратушняк, М.
Смирнов, В. Юкин. Методы сжатия данных. М. Диалог-МИФИ. 2002.
Гюнтер Борн. Форматы данных. Киев. Торгово-издательское бюро BHV. 1995.
Алгоритмы сжатия изображений. Форматы представления изображений
Фрактальное сжатие
Фрактальное сжатие, практически не имеет конкурентов по качеству сжатия для довольно широкого класса изображений, но его использование сдерживается медленной скоростью реализации данного алгоритма. Существуют многочисленные работы, призванные ускорить данный алгоритм.
Фрактальными множествами называются множества, обладающие следующими свойствами:
3. Самоподобие
4. Хаусдорфова размерность множества не целая
Рисунок 1. Этапы построения снежинки
Коха
Под самоподобием понимается следующий факт: для любой части объекта найдется ее меньшая часть, в каком-то смысле подобная данной.
Хаусдорфовой или фрактальной размерностью объекта XÌ Rn называется r, определяемой следующим образом. Разобьем все пространство Rn на кубы со стороной h , вершины которых лежат в точках сетки (i1h, i2h, …, inh). Пусть Kh - объединение кубов с шагом h, имеющих непустое пересечение с X. Тогда определим
r=lim h®0 log |Kh| / log h (если такой предел существует)
Например, на плоскости для отрезка [(0,0), (0,1)] имеем:
|Kh|= 2 é1/hù h2=2h(1+o(1))
log |Kh| / log h= log (2h(1+o(1))) / log h=1+ log (2(1+o(1))) / log h
lim h®0 log |Kh| / log h=1
Оказывается, что подавляющее большинство природных объектов обладают свойством фрактальности. С другой стороны, объекты созданные человеком, редко обладают этим свойством. Фрактальное сжатие активно использует свойство самоподобия изображений. При этом оказывается, что изображения природных объектов (например, изображение леса) поддаются фрактальному сжатию существенно лучше, чем, например, городской ландшафт.
Основная идея фрактального сжатия заключается в следующем. Рассмотрим для простоты серое изображение. График изображения, как график функции двух переменных, является объектом трехмерного пространства. Попробуем найти сжимающее отображение, переводящее данный график в себя. Вместо функции будет хранить некоторое описание этого сжимающего отображения.
Естественно, что таких отображений существует много. Мы будем искать отображение среди отображений в некотором классе. При этом оказывается, что такого отображения может вообще не существовать и мы будем искать отображение, переводящие изображение в некоторое близкое к нему. Исходя из свойств отображения, мы сможем получить оценку на норму разности исходного изображения и неподвижной точки найденного сжимающего отображения через норму разности исходного отображения и его образа после применения к нему найденного отображения.
Рассматривается следующий класс сжимающих отображений. Изображение разбивается на квадраты со стороной m. Назовем данные квадраты малыми. Вместе с тем, изображение разбивается на квадраты со стороной 2m. Назовем такие квадраты большими. В рассматриваемом классе отображений график функции на каждом малом квадрате ti получается в результате некоторого аффинного преобразования Li из графика функции на некотором большом квадрате Ti .Естественно, что при этом аффинное преобразование Li имеем вид
é a b 0ù
é xù é fù
Li (x,y,z)= ê c d 0 ê
ê y
ê
+ ê g ê
ë 0 0 e û ë z û ë hû
a b
Матрица c d задает аффинное преобразование, отображающее большой квадрат в малый. Легко увидеть, что таких отображение всего 8. Остается одномерное преобразование ez+h , перемещающее график изображения по оси Z. Это отображение задается двумя коэффициентами e, z. Условие сжимаемости: z<1.
Итак, для изображения размером M´N для каждого малого квадрата для задания отображения следует выделить 3 бита для преобразования квадрата, log2M+log2N бит для задания номера большого квадрата, две ячейки для задания коэффициентов e, z.
Алгоритм поиска оптимального сжимающего отображения для каждого малого квадрата сводится к следующему. Необходимо перебрать все большие квадраты. Для каждого из них надо перебрать все 8 вариантов отображений квадратов. Для каждого из отображений следует вычислить оптимальные e, z. В результате, после вычисления образа полученного отображения, мы имеем норму разности полученного изображения и исходного на малом квадрате - e.
Изо всех вышеописанных вариантов надо выбрать вариант с минимальной величиной e. Данный вариант и будет отображением в рассматриваемый малый квадрат.
Осталось описать алгоритм вычисления e, z. Сначала функция с большого квадрата u проецируется на малый. Это можно сделать, например, осредняя значение функции в каждых четырех соседних точках. Задача свелась к минимизации по e, z следующего выражения
S (euij+z-vij)2 = e2S uij2 +ez 2S uij-e2S uijvij+z2m2-z2S vij +S vij2
Беря частные производные по e и z, получим систему уравнений 2´2:
e 2S uij2 +z 2S uij=2S uijvij
e 2S uij +z2m2 =2S vij
Итого, у нас есть всего M/m N/m малых квадратов и M/2/m N/2/m больших. Для каждого малого квадрата и для каждого большого надо перебрать 8 вариантов отображений и для каждого время вычисления оптимального отображения есть O(m2). Т.о. суммарное время работы алгоритма
T(M,N,m) = O(M2N2/m2)
Существуют различные способы ускорения алгоритма. Основным из них – введения понятие индекса квадрата. Индексом называется разбиение множества всевозможных функций на квадрате на классы эквивалентности такие, что удачное сжимающее отображение может существовать только в случае, когда образ и прообраз отображения лежат в одном классе эквивалентности. Тогда для каждого малого квадрата поиск ведется только среди больших квадратов своего класса эквивалентности.
Существуют алгоритмы, когда малые квадраты имеют непостоянный размер. Т.е. если для данного размера малого квадрата не удалось найти удачного большого квадрата, то малый квадрат может разбиваться на подквадраты и для них будет применен тот же алгоритм поиска.
Шпаргалка для контрольной работы
struct
BMPHEAD
{
unsigned short int Signature
; //
Must be 0x4d42 == ”BM” //0
unsigned long FileLength
; // в байтах //2
unsigned long Zero ; // Must be 0 //6
unsigned long Ptr ; // смещение к области данных //10
unsigned long Version ;// длина оставшейся части
заголовка=0x28 //14
unsigned long Width ;
// ширина изображения в
пикселах //18
unsigned long Height ; //
высота изображения в пикселах //22
unsigned short int
Planes ; //
к-во битовых плоскостей //26
unsigned short int
BitsPerPixel ; // к-во
бит на папиксел //28
unsigned long Compression ; // сжатие: 0 или 1 или 2 //30
unsigned long SizeImage ; // размер блока данных в байтах //34
unsigned long XPelsPerMeter ; // в ширину: пикселов на метр //38
unsigned long YPelsPerMeter ; // в высчоту: пикселов на метр //42
unsigned long ClrUsed ; // к-во цветов в палитре //46
unsigned long ClrImportant ; // к-во используемых
цветов в палитре //50
} ;
FILE *fopen( const char *filename,
”rb+”);
size_t fread( void *buffer,
size_t size, size_t count, FILE
*stream );
fflush(FILE *f);
size_t fwrite( const void *buffer,
size_t size, size_t count, FILE
*stream );
long ftell( FILE *stream
);
int fseek( FILE *stream,
long offset, int origin );
origin:
SEEK_CUR, SEEK_END, SEEK_SET
fclose(f);
Пример задачи для контрольной
работы.
Известно, что обрабатываемый BMP-файл имеет 8 бит на пиксел и то, что он задается в серой
палитре (т.е. значение пиксела задает яркость). Требуется нарисовать в данном
изображении черный крест с центром в позиции (i,j). Имя BMP-файла и
значения i, j задаются в виде параметров
программы. Пример вызова программы:
./prog pic.bmp 10 10
При работе следует модифицировать существующий файл, т.е. открывать его
на чтение с модификацией.
Следующая функция ставит черную точку на черно-белом изображении (1 бит
на пиксел):
void SetPixel(FILE *f,
int i,int j, int width, int height, int ptr)
{char c=0;
fflush(f);
fseek(f,ptr+i*width+j/8,SEEK_SET);
fread(&c,1,1,f);
fflush(f);
c&=~(1<<(7-(j%8)));
fseek(f,ptr+i*width+j/8,SEEK_SET);
fwrite(&c,1,1,f);
}
Здесь:
f указатель на поток ввода/вывода
i номер строки изображения
j номер колонки изображения
width количество байт, используемое для хранения одной строки изображения в BMP-формате
height высота
изображения
ptr номер байта файла, с которого начинаются данные.
Простейшая реализация вышеуказанной задачи укладывается в следующую
программу:
int main( int
npar,char **par)
{
FILE *f; int width,height,ptr,
width_at_disk,i,j,i0,i1,j0,j1,bpp,ii,jj;
sscanf(par[2],"%d",&i); sscanf(par[3],"%d",&j); printf("i=%d j=%d\n",i,j);
f=fopen(par[1],"rb+");
fseek( f, 28, SEEK_SET ); fread(&bpp,1,sizeof(int),f);
fseek( f, 18, SEEK_SET );
fread(&width,1,sizeof(int),f);
fread(&height,1,sizeof(int),f);
fseek( f, 10, SEEK_SET ); fread(&ptr,1,sizeof(int),f);
width_at_disk=((width+7)/8+3)/4*4;
fseek( f, ptr, SEEK_SET );
i0=i-3; if(i0<0)i0=0; i1=i+3; if(i1>=height)i1=height-1;
j0=j-3; if(j0<0)j0=0; j1=j+3; if(j1>=width)j1=width-1;
for(ii=i0;ii<=i1;ii++) SetPixel(f,ii,j,
width_at_disk,height,ptr);
for(jj=j0;jj<=j1;jj++) SetPixel(f,i,jj,
width_at_disk,height,ptr);
fclose(f);
return 0;
}
Сжатие видео-изображений
Мы не будем далее
упоминать о том, что при сжатии видео-изображений вместе с видеорядом
приходится сжимать и аудио-информацию. Следует только отметить, что проблема
синхронизации изображения и звука является весьма важной проблемой.
Действительно, допустим, что декодер не успел раскодировать некоторый кадр и
перешел сразу к следующему. При этом должен быть обеспечен соответствующий
переход аудио-ряда.
При работе с графическими
изображениями для сжатия мы использовали два основных свойства изображений:
·
гладкое изменение цвета и яркости изображений
·
избыточность информации о изображении в цветовых
плоскостях (при соответствующем представлении цвета, например, YUV мы можем компоненты, отвечающие за цвет задавать более грубо, чем компоненту,
отвечающую за яркость изображения).
При рассмотрении
видео-изображений мы, также, можем использовать информацию о близости
изображений, отвечающих близким моментам времени.
Стандарты передачи видео-изображений
В Европе – PAL и SECAM.
Во обоих форматах яркость кодируется одинаково:
Y = 0.299R + 0.587G + 0.114B
Количество строк и частота кадров также совпадают, поэтому плееры, понимающие один формат, поймут и другой, но только в черно-белом цвете.
Цвет представляется по-разному.
SECAM появился в 1967 году во Франции и СССР. Формат распространен, в основном, в странах, на развитие которых оказывал сильной влияние СССР.
625 строк
(реально, на телевизорах видно меньше – 576 строк), 25 кадров в секунду. В
четных строках передается информация о R-Y
компонентах, а в нечетных – о B-Y компонентах. Декодер
повторяет каждую строку дважды для получения недостающей информации о R и B компонентах. Хотя четкость при этом снижается,
зато происходит полное разделение яркостных и цветовых компонент.
PAL появился в интервале с 1953 до 1967 года в ряде Европейских стран. Амплитуда несущего сигнала меняет знак через строку, поэтому помехи, вносимые в сигнал для каждой строки компенсируются на следующей строке.
NTSC появился в 1953 в США. Имеет частоту 30 кадров/сек., что должно уменьшать мерцание. С другой стороны, это усложняет преобразование сигнала на 50-герцовых телевизорах. 525 строк. Используется представление цвета YIQ (I –зелено-фиолетовый, Q-оранжево-цианитовый). Яркость представляется также как ив PAL/SECAM. Проблема: при колебаниях яркости за счет ошибок дискретизации при восстановления цветов цвета могут плавать.
Motion-JPEG
Этот стандарт является простым применением JPEG-сжатия для каждого отдельного кадра изображения.
MPEG
Существует несколько версий этого формата (MPEG-1, MPEG-2, MPEG-4, MPEG-7). В основе стандарта лежит все тот же алгоритм, что и в случае JPEG-сжатия.
Основные идеи следующие. Используется палитра YUV. Изображение разбивается на блоки 8x8 пикселов. По цветовым компонентам используется разрешение вдвое меньшее. В основе кодирования лежать макроблоки, состоящие из четырех соседних блоков по яркости и по одному блоку по цветовым компонентам. Этот подход сразу уменьшает вдвое объем информации.
Рассматривается 4 типа кадров:
I-кадры – (Intra pictures) – кадры, сжимающиеся независимо о соседних кадров.
P-кадры – (Predicted pictures) – кадры, сжимающиеся с использованием одного соседнего кадра.
B-кадры – (Bidirectional Predicted pictures) – кадры, сжимающиеся с использованием двух соседних кадров. Причем, эти кадры не должны использоваться для создания других кадров.
Т.о. для создания P-кадров и B-кадров можно
использовать I-кадры
и P-кадры.
Последовательность кадров может быть такой:
IBBPBBPBBPBBIBBPBBPBBPBBI…
Или для меньшего сжатия такой:
IBPBPBPBIBPBPBPBI…
Для первой последовательности при архивации кадра 1 используются кадры 0 и 3 . При архивации кадра 2 используются кадры 0 и 3 . . При архивации кадра 3 используется кадр 0 .
При разархивации изображения мы должны использовать для каждого очередного кадра уже разархивированные кадры. Поэтому для первого случая последовательность кадров должна быть следующей:
0 3 1 2 6 4 5 9 7 8 12 10
11…
для второй последовательности последовательность кадров должна быть следующей:
0 2 1 4 3 6 5 8 7 …
Вид архивации (I, P, B) задается отдельно для каждого макроблока изображения. Это значит, что в P-кадре встречаются I-макроблоки P-макроблоки. В B-кадре встречаются I-макроблок, P-макроблоки и B-макроблоки.
При архивации каждого макроблока используется макроблок с соседнего изображения. При этом, может быть использован макроблок с другими координатами, т.е. для каждого макроблока задается смещение к макроблоку, использующемуся для архивации данного макроблока. Более того, оказывается полезным добавить пару бит к полям, в которых задается смещение к исходным макроблокам, и допустить смещения, кратные полупикселу (т.е. к каждой координате смещения добавляется один бит). Понятно, что процедура поиска для каждого макроблока похожего макроблока из исходного изображения весьма дорогостояща.
Интересным способом улучшения сжатия является предварительная обработка видеосигнала. Известно, что вокруг областей резкого изменения яркости и цвета на изображении в процессе сжатия образуются артефакты (например, ореолы). Изображение можно незначительно сгладить так, что артефакты существенно уменьшатся, а внешний вид изображения практически не исказится.
Все вышеописанные моменты нашли свое отражение в стандарте MPEG-1.
Дальнейшим развитием этого направления стал стандарт MPEG-2.
Стандарт MPEG-4 представляет собой нечто принципиально новое, по сравнению с предыдущими версиями MPEG. В нем появляется понятие объектно-ориентированного языка BIFS, на котором можно писать псевдо-программы и внедрять их в код. Таким образом можно очень компактно передавать изображения, созданные программно – текст (например субтитры), отдельные статические изображения (например, логотипы). Таким же образом можно кодировать, например, трехмерные изображения, например, в мультфильмах, если они изначально кодировались в данном формате.
Наличие большого количества возможностей усложняет процесс написания соответствующих декодеров. Для решения этой проблемы введено понятие профилей. Профиль представляющих собой некий стандартных набор функций. Каждый видеоряд кодируется функциями из некоторого профиля. В каждом декодере записаны имена профилей, доступных данному декодеру. Тогда, если профиль видеоряда попадает в список профилей декодера, то декодер должен распознать данный видеоряд. Иначе выдается сообщение об ошибке.
Лекция 8
Области видимости и время жизни переменных в языке С
С точки зрения области видимости:
· Глобальные переменные
· Локальные в файле переменные
· Локальные переменные
С точки зрения времени жизни:
· Статические переменные
· Автоматические переменные
Кроме этого, в языке С существует возможность управления временем жизни переменных с помощью функций malloc и free. Переменные, созданные таким образом принято называть динамическими. Отметим, что как таковых этих переменных не существует, а существуют только указатели на них.
void *malloc( size_t size );
void *calloc( size_t num,
size_t size );
void *realloc( void *memblock,
size_t size );
void free( void *memblock );
Алгоритмы динамического выделения памяти
Существуют различные алгоритмы выделения/освобождения памяти.
Использование стека задачи
Существуют ситуации, когда есть
гарантия того, что память освобождаться в строго обратном порядке ее отведению.
Например, эта ситуация реализуется при отведении памяти под локальные
автоматические переменные в языке С. Действительно, для этих переменных память
отводится при входе в некоторый блок А, а освобождается при выходе из
блока А. При этом, память, отведенная под все переменные, находящиеся
во внутренних блоках блока А, отводится после отведения памяти переменных блока А, а освобождается до освобождения переменных блока А.
В этом случае переменные могут размещаться в стеке данной задачи. Компилятор видит определения всех локальных переменных в данном ядре, поэтому при появлении в блоке каждой локальной переменной компилятор ассоциирует ее с текущей позицией стека и перемещает указатель стека на размер этой переменной. При обработке куска кода внутри блока, компилятор преобразует все ссылки на локальные переменные в ссылки на соответствующие адреса внутри стека (т.е. у него есть таблица адресов локальных переменных для каждого блока). При выходе из блока, в соответствии с таблицей локальных переменных блока, компилятор отодвигает указатель на стек назад на размер локальных переменных в блоке.
Все остальные алгоритмы базируются на использовании общей кучи (heap) – линейного куска памяти с произвольным обращением по адресу.
Списки блоков фиксированного размера
Рассмотрим простейшую ситуацию. Пусть нам требуется выделять блоки памяти фиксированного размера L. Тогда напрашивается элементарное решение: объединить все свободные блоки в список свободного места. Элементом списка будет один блок. В каждый блок нам придется поместить указатели на предыдущий и следующий элементы списка.
Поиск свободного места (т.е. поиск свободного блока длиной L) становится элементарным: мы просто берем первый попавшийся блок в списке и исключаем его из списка свободного места. Освобождение памяти не сложнее: мы добавляем блок к списку свободного места.
Подобный механизм отведения памяти часто используется, например, при работе с жесткими дисками. Неиспользуемая дисковая память во многих файловых системах объединяется в список блоков.
Алгоритм близнецов (для блоков размером 2k)
Если существует необходимость иметь блоки нескольких размеров, то эту задачу можно свести к предыдущей: мы просто создадим отдельный список свободных блоков для каждого размера. На этом основан алгоритм близнецов.
Алгоритм предполагает, что будут выделяться блоки размером только 2k. В каждом таком блоке следует выделить служебную область. По сути, требуется всего один бит, указывающий: занят ли данный блок, или нет. В реальных ЭВМ обычно адресация возможна только к большим кускам памяти (например, к одному байту), поэтому и служебная область будет больше одного бита (как минимум, один байт).
Для каждого размера блока 2k создается двунаправленный список Listk свободных блоков размером 2k. Т.е. для каждого свободного блока в блоке вводятся три дополнительных служебных поля: указатели на предыдущий и следующий блоки в Listk и переменная со значением k, задающим размер блока. Списки реализуются с помощью фиктивного головного элемента.
Предполагается, что размер всей отведенной памяти равен M=2N и рассматриваются блоки длиной не менее m=2n.
В начальный момент все списки Listk пусты, кроме ListN , в котором располагается всего один элемент.
Алгоритм отведения блока памяти размером 2k следующий: если список Listk не пуст, то мы просто берем в нем первый элемент, исключаем из списка, помечаем его как занятый и используем для работы (например, возвращаем его адрес пользователю; если пользователь не знает о внутренней структуре алгоритма, то возвращаем адрес рабочей части блока).
Если список пуст, то мы рекурсивно отводим блок памяти размером 2k+1. Если это невозможно, сообщаем, что память отвести нельзя (например, функция отведения памяти возвращает NULL; в глубине рекурсии это может произойти только, если потребуется отвести блок памяти размером 2N+1). Блок размером 2k+1 разбиваем на две половины. Эти половины называются близнецами. Первую из этих половин добавляем в список свободных блоков размером 2k, а вторую – помечаем как занятый блок и используем для работы.
Легко увидеть, что алгоритм отведения памяти выполняется за время
T=O(N-n)=O(log M – log m).
Для освобождения памяти, занятой под блок, нам необходимо знать адрес начала блока (если пользователь получил адрес рабочей части блока, то, зная ее смещение, относительно начала блока, адрес начала блока легко получить). Пусть исходный блок размером 2N начинается с ячейки памяти с адресом 0.
Освобождение памяти базируется на следующем факте: для каждого блока мы можем легко найти адрес его блока-близнеца. Действительно, блоки близнецы размером 2k объединены в блок размером 2k+1. Адреса блоков размером 2k+1 кратны 2k+1 (легко доказать по индукции: для самого большого блока это верно; пусть это верно для блоков размером 2k+1, но блоки размером 2k располагаются либо в начале блоков размером 2k+1 с нулевым смещением, либо со смещением 2k , что и доказывает утверждение). Получаем, что в двоичном представлении адреса блока размером 2k+1 имеется k+1 нулей в младших битах. Соответствующие блоки-близнецы размером 2k из данного блока B размером 2k+1 имеют либо тот же самый адрес что и блок B, либо тот же адрес, в котором в k позиции прописана 1 (нумерация с нулевой позиции). Т.о. адрес блока близнеца Addr2 для блока с адресом Addr1 вычисляется по формуле:
Addr2=Addr1^(1<<k);
Если требует освободить блок с адресом Addr1, то мы ищем его блок-близнец. Если близнец оказывается занят или его не существует (это возможно только для блока размером 2N), то все, что нам остается, это – добавить блок с адресом Addr1 к списку свободных блоков соответствующего размера k (размер блока указан в служебной области блока). Если близнец свободен, то мы извлекаем его из списка Listk , объединяем данный блок и его близнец в блок размером 2k+1 (все, что для этого надо сделать – в первом из двух блоков увеличить на 1 значение поля, задающего длину блока) и рекурсивно применяем эту же процедуру для освобождения нового блока с размером 2k+1.
Легко увидеть, что асимптотика максимального времени работы алгоритма освобождения памяти совпадает с асимптотикой времени работы алгоритма отведения памяти. Т.о. алгоритм показывает очень хорошую скорость работы, но не позволяет отводить блоки памяти произвольного размера. В определенных ситуациях на последнее можно закрыть глаза. Т.е. если требуется выделить кусок памяти длиной l, то можно отводить кусок памяти длиной 2élog lù. Легко увидеть, что при этом размер лишней памяти (=l -2élog lù) не превосходит размера требуемой памяти.
В ОС Linux данный алгоритм используется в ядре системы как один из алгоритмов отведения памяти (функция kalloc).
Списки блоков свободной памяти в общем случае
В общем случае мы можем организовать свободную память в виде двухсвязного списка блоков. Кроме указателей на предыдущий и следующий элементы списка, в блоке будем хранить его длину. Если требуется выделить новый кусок памяти длиной l, то нам придется пролистать список до первого устраивающего нас блока. Далее, если l меньше длины найденного блока lb, то мы устанавливаем новую длину блока равной lb –l и оставшийся кусок длины l предоставляем для использования. Если l совпадает с lb, то мы просто исключаем данный блок из списка свободного места.
Существуют разные стратегии поиска подходящего блока. Две основные это: поиск первого подходящего (first fit) и наилучшего (best fit). При реализации стратегии first fit ищется первый блок, для которого lb ³ l . При реализации стратегии best fit ищется блок, для которого lb –l минимально среди всех блоков, для которых lb ³ l .
Алгоритмы отведения памяти, основанные на стратегии best fit , как правило, более экономичны (т.е. позволяют сохранять в течение большего времени большие блоки свободной памяти), но время работы таких алгоритмов прямо пропорционально длине списка. Время работы алгоритмов отведения памяти, основанных на стратегии first fit, зависит от распределения блоков длины не менее l среди всех блоков списка.
В указанной ситуации алгоритм очистки отведенной памяти (= алгоритм добавления блока в список + слияние его с соседними свободными блоками) оказывается также весьма дорогостоящим. Действительно, добавление блока в список выполняется за константу операций. Но, кроме этого, мы должны еще проверить – не свободны ли блоки памяти, стоящие непосредственно слева и справа от данного блока. Если они свободны, то требуется объединить эти блоки с данным блоком.
Т.о. суммарное время работы каждого из указанных алгоритмов T=O(L), где L – длина списка свободного места (в худшем случае).
Модифицированные списки блоков свободной памяти в общем случае (алгоритм парных меток)
Если мы готовы пойти на некоторые дополнительные накладные расходы, то скорость работы со списками свободной памяти можно существенно увеличить. Введем две дополнительные служебные ячейки памяти, расположенные в начале и конце блока (эти ячейки будут использоваться как в свободных, так и в занятых блоках). Договоримся, что для свободных блоков мы будем хранить в этих ячейках размер блока, а для занятых ячеек будем хранить размер блока со знаком `минус’. Эти ячейки называются парными метками.
Пространство между парными метками будем называть рабочей областью блока. Адрес именно этой части блока будет возвращаться пользователю. Соответственно, когда пользователь захочет освободить память, то именно этот адрес он передаст в программу освобождения памяти.
Как и ранее, в свободных блоках будут также храниться указатели на предыдущий и следующий блоки в списке свободного места.
Пусть h – размер машинного слова, т.е. размер переменной, в которой может размещаться адрес или длина любого объекта в памяти. Например, сейчас для обычных персональных компьютеров h=4 (в байтах).
Итак, если мы имеем адрес рабочей области отведенной памяти Addr, то по адресу Addr-h располагается длина данного блока памяти. В терминах языка С длина данного блока памяти это: *((int*)(((char*)Addr)-h)) или ((int*)Addr)[-1]. Здесь мы предположили, что длина любого объекта в памяти (а следовательно и адрес памяти) может размещаться в переменной типа int.
Можно сразу договориться, что длину блока мы будем измерять в машинных словах, т.е. в пересчете на размер переменной типа int. Тогда, размер блока будет также лежать в переменной ((int*)Addr)[((int*)Addr)[-1]-2]. Размер этой переменной должен быть на 2 больше размера рабочей части блока.
Для отведения памяти мы должны использовать ту же процедуру отведения памяти, что и для списков блоков свободной памяти в общем случае. Естественно, не надо забывать, что каждый блок должен быть погружен в парные метки, т.е. реально для каждого блока требуется на две ячейки памяти больше (на две переменные типа int), чем требуется пользователю.
Для очистки памяти мы можем использовать существенно более быструю процедуру. Для этого сначала, мы должны определить – нет ли свободных блоков непосредственно слева и справа от данного блока. Если соседние блоки заняты, то все, что надо сделать, это – добавить текущий блок к списку свободного места. Иначе, текущий блок следует объединить со свободными соседями и добавить получившийся блок к списку свободного места.
Более точно, существует четыре возможных ситуации, задающиеся знаками переменных ((int*)Addr)[-2] и ((int*)Addr)[((int*)Addr)[-1]-1].
1) Оба соседа заняты (((int*)Addr)[-2]<0 и ((int*)Addr)[((int*)Addr)[-1]-1]<0). Добавляем текущий блок к списку свободного места.
2) Блок слева свободен, блок справа занят (((int*)Addr)[-2]>0 и ((int*)Addr)[((int*)Addr)[-1]-1]<0). Если мы имеем адрес рабочей части удаляемого блока Addr, то размер левого блока содержится в переменной ((int*)Addr)[-2]. Левый блок принадлежит списку свободного места. Мы можем присоединить текущий блок к левому, не изменяя списка. Для этого надо только модифицировать парные метки блока, полученного объединением левого и текущего блоков. Т.е. в переменные ((int*)Addr)[((int*)Addr)[-1]-2], ((int*)Addr)[-2-((int*)Addr)[-2]+1] следует внести длину объединения двух блоков l2=((int*)Addr)[-1]+ ((int*)Addr)[-2].
3) Блок справа свободен, блок слева занят(((int*)Addr)[-2]<0 и ((int*)Addr)[((int*)Addr)[-1]-1]>0). Будем предполагать, что в свободном блоке указатели на предыдущий и следующий блоки лежат в указанном порядке в начале рабочей области блока (т.е. сразу после его длины). По сути, требуется исключить из списка правый блок, объединить текущий блок с правым и добавить их объединение к списку свободных блоков. Более коротко: можно скорректировать ссылки предыдущего и следующего блоков для правого блока, на текущий блок; установить ссылки на предыдущий и следующий блоки для текущего блока; модифицировать длину текущего блока:
int *right=((int*)Addr)+((int*)Addr)[-1]; // Указатель на рабочую часть правого блока
int *prev=((int**)right)[0]; // Указатель на пред. блок правого блока
int *next=((int**)right)[1]; // Указатель на след. блок правого блока
((int**)prev)[2]= ((int*)Addr)-1; //предыдущий->следующий := текущий
((int**)next)[1]= ((int*)Addr)-1; //следующий->предыдущий := текущий
((int**)Addr)[0]=prev; // текущий-> предыдущий := предыдущий
((int**)Addr)[1]=next; // текущий->следующий := следующий
((int*)Addr)[-1]+= ((int*)Addr)[((int*)Addr)[-1]-1]; // длина=сумме длин
((int*)Addr)[((int*)Addr)[-1]-2]= ((int*)Addr)[-1];
4) Блоки справа и слева свободны (((int*)Addr)[-2]>0 и ((int*)Addr)[((int*)Addr)[-1]-1]>0). Исключим правый блок из списка, а затем объединим левый, текущий и правый блоки:
int *right=((int*)Addr)+((int*)Addr)[-1]; // Указатель на рабочую часть правого блока
int *prev=((int**)right)[0]; // Указатель на пред. блок правого блока
int *next=((int**)right)[1]; // Указатель на след. блок правого блока
((int**)prev)[2]=next; //предыдущий->следующий := следующий
((int**)next)[1]=prev; //следующий->предыдущий := предыдущий
int l2=((int*)Addr)[-2]+ ((int*)Addr)[-1]+(((int*)Addr)+((int*)Addr)[-1])[-1];
((int*)Addr)[-((int*)Addr)[-2]-1]=l2;
((int*)Addr)[-((int*)Addr)[-2]-1+l2-1]=l2;
Отметим, что мы использовали в формулах тот факт, что sizeof(int)==sizeof(int*). Следует попрактиковаться и выписать соответствующие формулы, если это не так.
Гарантируется наличие ошибок в
вышеприведенных формулах J.
Сборка мусора
Возможна принципиально другая стратегия выделения/освобождения памяти. Согласно этой стратегии, мы можем создавать объекты, но не имеем возможности их удалять. В этом случае в среде, в которой происходит выполнение программы, должен присутствовать механизм, называемый сборкой мусора. Память выделяется до тех пор, пока хватает системных ресурсов. Когда ресурсы заканчиваются запускается процесс сборки мусора, который освобождает память из под всех объектов, на которые не ссылаются никакие переменные из программы. Например, в рамках этой идеологии реализован язык программирования Java.
Простейшей реализацией системы сборки мусора является введение для каждого объекта счетчика ссылок на него. Если какая-то переменная становится ссылкой на объект, то счетчик ссылок увеличивается на 1. Если какая-то переменная уничтожается или становится ссылкой на другой объект, то счетчик на первоначальный объект уменьшается на 1. Считается, что объект, на который никто не ссылается уже никому и не нужен, поэтому он уничтожается в процессе сборки мусора. Подобный подход реализован в языке Perl. Уничтожение объекта происходит сразу же в момент, когда счетчик обнуляется.
Данная реализация имеет очевидные проблемы: если отвести память под циклический список, а потом уничтожить ссылку на этот список, то на каждый объект списка все равно будет ссылаться предыдущий в списке элемент. Т.е. при подобном подходе список уничтожен не будет. Более того, даже если система обнаружит, что на данный список нет больше ссылок, то удалить она его все равно не сможет, т.к. не знает, в каком порядке это надо делать.
Другой разновидностью алгоритмов сборки мусора являются алгоритмы трассировки. При реализации этого алгоритма система с некоторой частотой запускает процесс сборки мусора. При этом, основной процесс приостанавливается, чтобы не вносить путаницы. В каждом объекте вводится флаг, обозначающий – используется ли данный объект, или нет. В процессе сбора мусора сначала все флаги обнуляются. Далее рассматривается множество базовых салок, доступных в данный момент программе. В них флаг устанавливается равным 1. Далее процесс рекурсивно переходит к ссылкам, содержащимся в данных ссылках, и устанавливает флаги в них =1. И т.д. Естественно, что при этом, ссылки на объекты со значением флага, равным 1, далее не рассматриваются. Т.о., происходит проход по дереву зависимостей объектов. Когда ссылок не нулевыми флагами не останется, то запускается второй этап алгоритма. Просматриваются ссылки на все существующие объекты и объекты с нулевым значением флага добавляются в список свободной памяти.
Существенным недостатком данного подхода является то, что основной процесс приходится приостанавливать для реализации сборки мусора. Если память сильно загружена, то, с одной стороны, сборка мусора выполняется долга, а с другой – довольно часто. Данный подход лишает нас возможности автоматического вызова деструктора – функции, которая должна вызываться системой в момент разрушения объекта. Эти недостатки привели к остановке развития одного из самых сильных объектно-ориентированных языков – Java, в котором реализован данный подход.
Объектно-ориентированные языки
Три основных характеристики объектно-ориентированных языков программирования: инкапсуляция, полиморфизм, наследование.
Инкапсуляция
Инкапсуляцией называется способность локализовать некоторый набор переменных и функций внутри одного объекта. Рассмотрим следующую структуру в языке С++:
struct SString
{
int Length;
char str[256];
int Len(){return Length;}
};
Хотя мы определили структуру, а не класс, но все же следует иметь в виду, что структуры в языке С++ являются несколько упрощенной реализацией классов (на самом деле структура = класс, все переменные и функции которого объявлены как public). Поэтому мы вправе говорить, что мы определили некоторый класс.
Следует понимать, что отличие понятий класс и объект. Класс лишь описывает объект, не создавая его (т.е., например, не отводя память под объект). Создание класса = создание описания нового типа. Сам объект создается, когда мы создаем экземпляр класса :
SString str;
Обращаться к функциям класса (функции класса называются методами; вызовы методов класса называются сообщениями) можно также как и к переменным класса:
strcpy(str.str,”Hello”);
str.Length=strlen(str.str);
Переменные класса оказываются тесно привязанные к данному классу (а при создании объекта – к данному объекту). Из функций класса мы можем получить доступ к переменным данного класса. В идеале, мы можем сделать так, чтобы доступ к переменным класса был бы возможен только из функций данного класса.
Для управления доступом к переменным класса в языке С++ существуют ключевые слова private, protected, public:
class CString
{private:
int Length;
char *str;
public:
int Len(){return Length;}
void Set(char *str){Length=strlen(str);
this->str=strdup(str);}
char *GetStr(){return str;}
};
Извне возможен доступ к переменным и функциям класса, объявленным как public. В приведенном примере задавать значение переменных класса можно только через функции класса:
CString s;
s.Set(”Hello!!!”);
printf(”%s\n”,s.GetStr());
В данном примере показывается вариант идеальной инкапсуляции. В реальности для упрощения жизни часто разрешают доступ к некоторым переменным класса извне.
Наследование
Наследованием называется возможность создания новых (дочерних) классов на базе существующих (родительских) с наследованием всех или части свойств родительских классов:
class CString2
{protected:
int Length;
char *str;
public:
int Len(){return Length;}
void Set(char *str){Length=strlen(str);
this->str=strdup(str);}
char *GetStr(){return str;}
};
class CString3: public
CString2
{
int SumLetters(){int i,s=0;
for(i=0;i>Length;i++)s+=str[i]; return s;}
};
Класс CString3 наследует все методы и переменные класса CString2 и в нем появляется новая функция, считающая сумму кодов символов строки, заданной в классе CString2.
Здесь видно отличие спецификаций private и protected. В обоих случаях к переменным класса, имеющим данные спецификации, нельзя обращаться извне класса. Но к private переменным также нельзя обращаться и из порожденных классов, а к protected переменным – можно. Т.о. класс CString3 аналогичным образом нельзя было породить из класса CString. Хотя (в данном случае) можно было пойти `обходным’ путем:
class CString3_: public CString
{
int SumLetters(){int
i,s=0; for(i=0;i>Len();i++)s+=GetStr()[i]; return s;}
};
В указанных моментах кроется повод для некоторых нареканий на язык С++: базовые классы следует очень тщательно проектировать. Если впоследствии нам потребуется получить доступ в порожденных классах к приватным переменным родительского класса, то напрямую мы его уже никак получить не сможем, не меняя, при этом, родительского класса.
При наследовании:
class CString3: public
CString2
…
вместо ключевого слова public можно было указать другие ключевые слова: private или protected. В данном случае указывается способ наследования переменных класса. При способе наследования public публичность переменных не изменяется. При способе наследования protected публичность переменных не изменяется, кроме public переменных, которые становятся protected. При способе наследования private все переменные класса становятся private.
Полиморфизм
Полиморфизмом называется способность языка использовать различные функции и операторы с одинаковыми именами. Какой вариант функции при этом используется – зависит либо от контекста, либо от внутренних свойств класса, для которого вызывается соответствующий метод.
Полиморфизм бывает трех типов:
·
Включения
·
Операционный
·
Параметрический
Лекция 9
Списки блоков свободной памяти в общем случае
В общем случае мы можем организовать свободную память в виде двухсвязного списка блоков. Кроме указателей на предыдущий и следующий элементы списка, в блоке будем хранить его длину. Если требуется выделить новый кусок памяти длиной l, то нам придется пролистать список до первого устраивающего нас блока. Далее, если l меньше длины найденного блока lb, то мы устанавливаем новую длину блока равной lb –l и оставшийся кусок длины l предоставляем для использования. Если l совпадает с lb, то мы просто исключаем данный блок из списка свободного места.
Существуют разные стратегии поиска подходящего блока. Две основные это: поиск первого подходящего (first fit) и наилучшего (best fit). При реализации стратегии first fit ищется первый блок, для которого lb ³ l . При реализации стратегии best fit ищется блок, для которого lb –l минимально среди всех блоков, для которых lb ³ l .
Алгоритмы отведения памяти, основанные на стратегии best fit , как правило, более экономичны (т.е. позволяют сохранять в течение большего времени большие блоки свободной памяти), но время работы таких алгоритмов прямо пропорционально длине списка. Время работы алгоритмов отведения памяти, основанных на стратегии first fit, зависит от распределения блоков длины не менее l среди всех блоков списка.
В указанной ситуации алгоритм очистки отведенной памяти (= алгоритм добавления блока в список + слияние его с соседними свободными блоками) оказывается также весьма дорогостоящим. Действительно, добавление блока в список выполняется за константу операций. Но, кроме этого, мы должны еще проверить – не свободны ли блоки памяти, стоящие непосредственно слева и справа от данного блока. Если они свободны, то требуется объединить эти блоки с данным блоком.
Т.о. суммарное время работы каждого из указанных алгоритмов T=O(L), где L – длина списка свободного места (в худшем случае).
Модифицированные списки блоков свободной памяти в общем случае (алгоритм парных меток)
Если мы готовы пойти на некоторые дополнительные накладные расходы, то скорость работы со списками свободной памяти можно существенно увеличить. Введем две дополнительные служебные ячейки памяти, расположенные в начале и конце блока (эти ячейки будут использоваться как в свободных, так и в занятых блоках). Договоримся, что для свободных блоков мы будем хранить в этих ячейках размер блока, а для занятых ячеек будем хранить размер блока со знаком `минус’. Эти ячейки называются парными метками.
Пространство между парными метками будем называть рабочей областью блока. Адрес именно этой части блока будет возвращаться пользователю. Соответственно, когда пользователь захочет освободить память, то именно этот адрес он передаст в программу освобождения памяти.
Как и ранее, в свободных блоках будут также храниться указатели на предыдущий и следующий блоки в списке свободного места.
Пусть h – размер машинного слова, т.е. размер переменной, в которой может размещаться адрес или длина любого объекта в памяти. Например, сейчас для обычных персональных компьютеров h=4 (в байтах).
Итак, если мы имеем адрес рабочей области отведенной памяти Addr, то по адресу Addr-h располагается длина данного блока памяти. В терминах языка С длина данного блока памяти это: *((int*)(((char*)Addr)-h)) или ((int*)Addr)[-1]. Здесь мы предположили, что длина любого объекта в памяти (а следовательно и адрес памяти) может размещаться в переменной типа int.
Можно сразу договориться, что длину блока мы будем измерять в машинных словах, т.е. в пересчете на размер переменной типа int. Тогда, размер блока будет также лежать в переменной ((int*)Addr)[((int*)Addr)[-1]-2]. Размер этой переменной должен быть на 2 больше размера рабочей части блока.
Для отведения памяти мы должны использовать ту же процедуру отведения памяти, что и для списков блоков свободной памяти в общем случае. Естественно, не надо забывать, что каждый блок должен быть погружен в парные метки, т.е. реально для каждого блока требуется на две ячейки памяти больше (на две переменные типа int), чем требуется пользователю.
Для очистки памяти мы можем использовать существенно более быструю процедуру. Для этого сначала, мы должны определить – нет ли свободных блоков непосредственно слева и справа от данного блока. Если соседние блоки заняты, то все, что надо сделать, это – добавить текущий блок к списку свободного места. Иначе, текущий блок следует объединить со свободными соседями и добавить получившийся блок к списку свободного места.
Более точно, существует четыре возможных ситуации, задающиеся знаками переменных ((int*)Addr)[-2] и ((int*)Addr)[((int*)Addr)[-1]-1].
1) Оба соседа заняты (((int*)Addr)[-2]<0 и ((int*)Addr)[((int*)Addr)[-1]-1]<0). Добавляем текущий блок к списку свободного места.
2) Блок слева свободен, блок справа занят (((int*)Addr)[-2]>0 и ((int*)Addr)[((int*)Addr)[-1]-1]<0). Если мы имеем адрес рабочей части удаляемого блока Addr, то размер левого блока содержится в переменной ((int*)Addr)[-2]. Левый блок принадлежит списку свободного места. Мы можем присоединить текущий блок к левому, не изменяя списка. Для этого надо только модифицировать парные метки блока, полученного объединением левого и текущего блоков. Т.е. в переменные ((int*)Addr)[((int*)Addr)[-1]-2], ((int*)Addr)[-2-((int*)Addr)[-2]+1] следует внести длину объединения двух блоков l2=((int*)Addr)[-1]+ ((int*)Addr)[-2].
3) Блок справа свободен, блок слева занят(((int*)Addr)[-2]<0 и ((int*)Addr)[((int*)Addr)[-1]-1]>0). Будем предполагать, что в свободном блоке указатели на предыдущий и следующий блоки лежат в указанном порядке в начале рабочей области блока (т.е. сразу после его длины). По сути, требуется исключить из списка правый блок, объединить текущий блок с правым и добавить их объединение к списку свободных блоков. Более коротко: можно скорректировать ссылки предыдущего и следующего блоков для правого блока, на текущий блок; установить ссылки на предыдущий и следующий блоки для текущего блока; модифицировать длину текущего блока:
int *right=((int*)Addr)+((int*)Addr)[-1]; // Указатель на рабочую часть правого блока
int *prev=((int**)right)[0]; // Указатель на пред. блок правого блока
int *next=((int**)right)[1]; // Указатель на след. блок правого блока
((int**)prev)[2]= ((int*)Addr)-1; //предыдущий->следующий := текущий
((int**)next)[1]= ((int*)Addr)-1; //следующий->предыдущий := текущий
((int**)Addr)[0]=prev; // текущий-> предыдущий := предыдущий
((int**)Addr)[1]=next; // текущий->следующий := следующий
((int*)Addr)[-1]+= ((int*)Addr)[((int*)Addr)[-1]-1]; // длина=сумме длин
((int*)Addr)[((int*)Addr)[-1]-2]= ((int*)Addr)[-1];
4) Блоки справа и слева свободны (((int*)Addr)[-2]>0 и ((int*)Addr)[((int*)Addr)[-1]-1]>0). Исключим правый блок из списка, а затем объединим левый, текущий и правый блоки:
int *right=((int*)Addr)+((int*)Addr)[-1]; // Указатель на рабочую часть правого блока
int *prev=((int**)right)[0]; // Указатель на пред. блок правого блока
int *next=((int**)right)[1]; // Указатель на след. блок правого блока
((int**)prev)[2]=next; //предыдущий->следующий := следующий
((int**)next)[1]=prev; //следующий->предыдущий := предыдущий
int l2=((int*)Addr)[-2]+ ((int*)Addr)[-1]+(((int*)Addr)+((int*)Addr)[-1])[-1];
((int*)Addr)[-((int*)Addr)[-2]-1]=l2;
((int*)Addr)[-((int*)Addr)[-2]-1+l2-1]=l2;
Отметим, что мы использовали в формулах тот факт, что sizeof(int)==sizeof(int*). Следует попрактиковаться и выписать соответствующие формулы, если это не так.
Гарантируется наличие ошибок в
вышеприведенных формулах J.
Сборка мусора
Возможна принципиально другая стратегия выделения/освобождения памяти. Согласно этой стратегии, мы можем создавать объекты, но не имеем возможности их удалять. В этом случае в среде, в которой происходит выполнение программы, должен присутствовать механизм, называемый сборкой мусора. Память выделяется до тех пор, пока хватает системных ресурсов. Когда ресурсы заканчиваются запускается процесс сборки мусора, который освобождает память из под всех объектов, на которые не ссылаются никакие переменные из программы. Например, в рамках этой идеологии реализован язык программирования Java.
Простейшей реализацией системы сборки мусора является введение для каждого объекта счетчика ссылок на него. Если какая-то переменная становится ссылкой на объект, то счетчик ссылок увеличивается на 1. Если какая-то переменная уничтожается или становится ссылкой на другой объект, то счетчик на первоначальный объект уменьшается на 1. Считается, что объект, на который никто не ссылается уже никому и не нужен, поэтому он уничтожается в процессе сборки мусора. Подобный подход реализован в языке Perl. Уничтожение объекта происходит сразу же в момент, когда счетчик обнуляется.
Данная реализация имеет очевидные проблемы: если отвести память под циклический список, а потом уничтожить ссылку на этот список, то на каждый объект списка все равно будет ссылаться предыдущий в списке элемент. Т.е. при подобном подходе список уничтожен не будет. Более того, даже если система обнаружит, что на данный список нет больше ссылок, то удалить она его все равно не сможет, т.к. не знает, в каком порядке это надо делать.
Другой разновидностью алгоритмов сборки мусора являются алгоритмы трассировки. При реализации этого алгоритма система с некоторой частотой запускает процесс сборки мусора. При этом, основной процесс приостанавливается, чтобы не вносить путаницы. В каждом объекте вводится флаг, обозначающий – используется ли данный объект, или нет. В процессе сбора мусора сначала все флаги обнуляются. Далее рассматривается множество базовых салок, доступных в данный момент программе. В них флаг устанавливается равным 1. Далее процесс рекурсивно переходит к ссылкам, содержащимся в данных ссылках, и устанавливает флаги в них =1. И т.д. Естественно, что при этом, ссылки на объекты со значением флага, равным 1, далее не рассматриваются. Т.о., происходит проход по дереву зависимостей объектов. Когда ссылок не нулевыми флагами не останется, то запускается второй этап алгоритма. Просматриваются ссылки на все существующие объекты и объекты с нулевым значением флага добавляются в список свободной памяти.
Существенным недостатком данного подхода является то, что основной процесс приходится приостанавливать для реализации сборки мусора. Если память сильно загружена, то, с одной стороны, сборка мусора выполняется долга, а с другой – довольно часто. Данный подход лишает нас возможности автоматического вызова деструктора – функции, которая должна вызываться системой в момент разрушения объекта. Эти недостатки привели к остановке развития одного из самых сильных объектно-ориентированных языков – Java, в котором реализован данный подход.
Объектно-ориентированные языки
Список литературы
Бьерн Страуструп. Язык программирования С++.
Три основных характеристики объектно-ориентированных языков программирования: инкапсуляция, полиморфизм, наследование.
Инкапсуляция
Инкапсуляцией называется способность локализовать некоторый набор переменных и функций внутри одного объекта. Рассмотрим следующую структуру в языке С++:
struct SString
{
int Length;
char str[256];
int Len(){return Length;}
};
Хотя мы определили структуру, а не класс, но все же следует иметь в виду, что структуры в языке С++ являются несколько упрощенной реализацией классов (на самом деле структура = класс, все переменные и функции которого объявлены как public). Поэтому мы вправе говорить, что мы определили некоторый класс.
Следует понимать, что отличие понятий класс и объект. Класс лишь описывает объект, не создавая его (т.е., например, не отводя память под объект). Создание класса = создание описания нового типа. Сам объект создается, когда мы создаем экземпляр класса :
SString str;
Обращаться к функциям класса (функции класса называются методами; вызовы методов класса называются сообщениями) можно также как и к переменным класса:
strcpy(str.str,”Hello”);
str.Length=strlen(str.str);
Переменные класса оказываются тесно привязанные к данному классу (а при создании объекта – к данному объекту). Из функций класса мы можем получить доступ к переменным данного класса. В идеале, мы можем сделать так, чтобы доступ к переменным класса был бы возможен только из функций данного класса.
Для управления доступом к переменным класса в языке С++ существуют ключевые слова private, protected, public:
class CString
{private:
int Length;
char *str;
public:
int Len(){return Length;}
void Set(char *str){Length=strlen(str);
this->str=strdup(str);}
char *GetStr(){return str;}
};
Извне возможен доступ к переменным и функциям класса, объявленным как public. В приведенном примере задавать значение переменных класса можно только через функции класса:
CString s;
s.Set(”Hello!!!”);
printf(”%s\n”,s.GetStr());
В данном примере показывается вариант идеальной инкапсуляции. В реальности для упрощения жизни часто разрешают доступ к некоторым переменным класса извне.
Наследование
Наследованием называется возможность создания новых (дочерних) классов на базе существующих (родительских) с наследованием всех или части свойств родительских классов:
class CString2
{protected:
int Length;
char *str;
public:
int Len(){return Length;}
void Set(char *str){Length=strlen(str);
this->str=strdup(str);}
char *GetStr(){return str;}
};
class CString3: public
CString2
{
int SumLetters(){int i,s=0;
for(i=0;i>Length;i++)s+=str[i]; return s;}
};
Класс CString3
наследует все методы и переменные класса CString2 и в нем
появляется новая функция, считающая сумму кодов символов строки, заданной в
классе CString2.
Здесь видно отличие спецификаций private и protected. В обоих
случаях к переменным класса, имеющим данные спецификации, нельзя обращаться
извне класса. Но к private переменным
также нельзя обращаться и из порожденных классов, а к protected переменным – можно. Т.о. класс CString3
аналогичным образом нельзя было породить из класса CString.
Хотя (в данном случае) можно было пойти `обходным’
путем:
class CString3_:
public CString
{
int SumLetters(){int
i,s=0; for(i=0;i>Len();i++)s+=GetStr()[i]; return s;}
};
В указанных моментах кроется повод для некоторых нареканий на язык С++: базовые классы следует очень тщательно проектировать. Если впоследствии нам потребуется получить доступ в порожденных классах к приватным переменным родительского класса, то напрямую мы его уже никак получить не сможем, не меняя, при этом, родительского класса.
При наследовании:
class CString3: public
CString2
…
вместо ключевого слова public можно было указать другие ключевые слова: private или protected. В данном случае указывается способ наследования переменных класса. При способе наследования public публичность переменных не изменяется. При способе наследования protected публичность переменных не изменяется, кроме public переменных, которые становятся protected. При способе наследования private все переменные класса становятся private.
Полиморфизм
Полиморфизмом называется способность языка использовать различные функции и операторы с одинаковыми именами. Какой вариант функции при этом используется – зависит либо от контекста, либо от внутренних свойств класса, для которого вызывается соответствующий метод.
Полиморфизм бывает трех типов:
·
Включения
·
Операционный
·
Параметрический
Полиморфизм включения
Существует две основных разновидности способов определения, какую функцию следует вызывать при выполнении программы в ответ на просьбу пользователя вызвать функцию с определенным именем.
При использовании первой разновидности способов конкретная функция определяется а этапе компиляции, исходя из информации, скрытой в самой программе. Данный подход носит название статического связывания.
При использовании второй разновидности способов конкретная функция определяется в процессе выполнения, исходя из информации, получаемой при выполнении кода. Данный подход носит название динамического связывания. Именно этот подход используется в языке С++ для реализации полиморфизма включения.
Рассмотрим
следующий пример
#include <stdio.h>
class CBase
{public:
virtual void
test(){printf("virtual check: CBase\n");}
void
test2(){printf("standard check: CBase\n");}
};
class CChild1:public CBase
{public:
void test(){printf("virtual
check: CChild1\n");}
void
test2(){printf("standard check: CChild1\n");}
};
class CChild2:public CBase
{public:
void test(){printf("virtual
check: CChild2\n");}
void
test2(){printf("standard check: CChild2\n");}
};
main()
{CBase *m[3]; int i;
m[0]=new CBase;
m[1]=new CChild1;
m[2]=new CChild2;
for(i=0;i<3;i++)m[i]->test();
for(i=0;i<3;i++)m[i]->test2();
return 0;
}
Функция test2 реализована в базовом классе CBase и в дочерних от него классах CChild1, CChild2. При вызове метода test2 для объекта типа CBase вызывается соответствующая функция из класса CBase , если же метод test2 вызывается для дочернего класса, то вызывается соответствующая функция дочернего класса. Информацию о том, какую функцию следует вызывать, легко получить на этапе компиляции из информации о типе соответствующего объекта. Т.о. здесь используется обычное статическое связывание.
Ситуацию можно изменить следующим образом. Пусть у нас есть указатель типа CBase*. Мы можем присвоить этому указателю указатель на объект типа CBase, а можем присвоить указатель на объект типа CChild1 или CChild2. С точки зрения функции test2 это не меняет ситуацию – она будет вызываться для базового класса в любом случае (если вы, конечно, не измените тип указателя). Однако, если перед описанием функции приписать ключевое слово virtual , то это приведет к тому, что при поиске требуемой функции будет использоваться динамическое связывание. В приведенном примере функция test базового класса является виртуальной. Поэтому в самом объекте хранится информация о том, какого типа данный объект. Для виртуальной функции информация о типе объекта берется не из информации о типе, которая есть у компилятора (в нашем примере переменная m[i] имеет тип CBase*, следовательно m[i] указывает на объект типа CBase), а из информации внутри самого класса. Поэтому после инициализации
m[1]=new CChild1();
в структуре, на которую указывает m[1] содержится информация о типе данного объекта. При вызове m[i]->test(); эта информация будет использована для того, чтобы вызвать функцию test из соответствующего порожденного класса CChild1.
В результате на экран будет выведено:
virtual check: CBase
virtual check: CChild1
virtual check: CChild2
standard check: CBase
standard check: CBase
standard check: CBase
Полиморфизм операционный
Операционный полиморфизм использует механизм статического связывания. В языке в одном классе может быть несколько методов с одинаковыми именами, но разными параметрами. Подобный механизм называется механизмом перегрузки функций. Если используется механизм перегрузки функции, то для этой функции перестают действовать правила неявных преобразований типов для фактических параметров. При использовании перегрузки функций тип фактических параметров должен идеально совпадать с типом формальных параметров.
В реальности механизм перегрузки функций приводит к тому, что внутренне имя функции при компиляции программы состоит из собственно имени функции и из символов, задающих тип параметров функции. Это не соответствует способу внутреннего представления имен для языка С. Поэтому, вообще говоря, библиотечные функции, написанные на языке С (соответственно, при использовании компилятора с языка С) несовместимы с программами на языке С++. Ситуация решается введением ключевого слова `C’ (в разных компиляторах это слово может выглядеть несколько по-разному; например, в Microsoft Visual C++ для этих целей используется фраза extern "C"). С помощью данного ключевого слова можно указать компилятору, что внутренне имя для данной функции создавалось в соответствии с правилами языка С.
Полиморфизм параметрический
Часто требуется использовать несколько одинаковых функций (или классов), отличающихся лишь типом параметров. Простейший пример: функции минимума, максимума, абсолютного значения и т.д. В языке С в этом случае можно применять оператор препроцессора define:
#define
MIN(x,y) ((x)<(y)?(x):y))
но это не всегда удобно, т.к. полноценная функция при этом не создается.
В языке С++
для этих целей используются шаблоны или
template:
template<class c> c min(c x,c y){return ((x)<(y)?(x):y));}
Фактически компилятор создает различные варианты этой функции для каждого варианта фактических параметров этой функции. Например, пусть эта функция вызвана следующим образом:
printf("%g %d %lg\n",min(3.f,4.f),min(3,4),min(3.,4.));
тогда компилятор создает три функции:
float min(float x, float y){return ((x)<(y)?(x):y));}
int min(int x, int y){return ((x)<(y)?(x):y));}
double min(double x, double y){return ((x)<(y)?(x):y));}
и вызывает их в
соответствующих местах программы.
Конструкторы и деструкторы
Объекты рождаются и умирают. С этими событиями можно ассоциировать соответствующие функции: конструкторы и деструкторы. Конструктор автоматически вызывается в момент рождения объекта, а деструктор – в момент смерти.
Это очень удобно, т.к. дает возможность производить различные инициализации, с одной стороны, и очистку памяти после использования объекта, с другой.
Конструктором
считается функция, имеющая то же имя, что и имя класса. У деструктора то же
самое имя, но с символом `~’ перед именем функции. Например:
class CString
{
char *str; int l;
public:
CString(){l=256; str=new
char[l];}
CString(int l){this->l=l;
str=new char[l];}
~CString(){l=0; delete str;
str=NULL;}
};
CString s1,s2(1024);
Здесь мы создали две переменные. При создании первой переменной вызвался конструктор по умолчанию (без параметров), который отвел 256 ячеек памяти под строку. При создании второй переменой вызвался конструктор с целочисленным аргументом, который отвел 1024 ячеек памяти под строку. Память будет освобождена при смерти обеих переменных.
Лекция 10
Объектно-ориентированные языки
Список литературы
Бьерн Страуструп. Язык программирования С++.
Главы, помеченные
звездочкой не обязательны для прочтения, но обязательны для минимального
понимания языка С++.
Три основных характеристики объектно-ориентированных языков программирования: инкапсуляция, полиморфизм, наследование.
Инкапсуляция
Инкапсуляцией называется способность локализовать некоторый набор переменных и функций внутри одного объекта. Рассмотрим следующую структуру в языке С++:
struct SString
{
int Length;
char str[256];
int Len(){return Length;}
};
Хотя мы определили структуру, а не класс, но все же следует иметь в виду, что структуры в языке С++ являются несколько упрощенной реализацией классов (на самом деле структура = класс, все переменные и функции которого объявлены как public). Поэтому мы вправе говорить, что мы определили некоторый класс.
Следует понимать, что отличие понятий класс и объект. Класс лишь описывает объект, не создавая его (т.е., например, не отводя память под объект). Создание класса = создание описания нового типа. Сам объект создается, когда мы создаем экземпляр класса :
SString str;
Обращаться к функциям класса
(функции класса называются методами; вызовы
методов класса называются сообщениями)
можно также как и к переменным класса:
strcpy(str.str,”Hello”);
str.Length=strlen(str.str);
Переменные класса оказываются тесно привязанные к данному классу (а при создании объекта – к данному объекту). Из функций класса мы можем получить доступ к переменным данного класса. В идеале, мы можем сделать так, чтобы доступ к переменным класса был бы возможен только из функций данного класса.
Для управления доступом к
переменным класса в языке С++ существуют ключевые слова private, protected, public:
class CString
{private:
int Length;
char *str;
public:
int Len(){return Length;}
void Set(char *str){Length=strlen(str);
this->str=strdup(str);}
char *GetStr(){return str;}
};
Извне возможен доступ к переменным и функциям класса, объявленным как public. В приведенном примере задавать значение переменных класса можно только через функции класса:
CString s;
s.Set(”Hello!!!”);
printf(”%s\n”,s.GetStr());
В данном примере показывается вариант идеальной инкапсуляции. В реальности для упрощения жизни часто разрешают доступ к некоторым переменным класса извне.
Наследование
Наследованием называется возможность создания новых (дочерних) классов на базе существующих (родительских) с наследованием всех или части свойств родительских классов:
class CString2
{protected:
int Length;
char *str;
public:
int Len(){return Length;}
void Set(char *str){Length=strlen(str);
this->str=strdup(str);}
char *GetStr(){return str;}
};
class CString3: public
CString2
{
int SumLetters(){int i,s=0;
for(i=0;i>Length;i++)s+=str[i]; return s;}
};
Класс CString3
наследует все методы и переменные класса CString2 и в нем
появляется новая функция, считающая сумму кодов символов строки, заданной в
классе CString2.
Здесь видно отличие спецификаций private и protected. В обоих
случаях к переменным класса, имеющим данные спецификации, нельзя обращаться
извне класса. Но к private переменным
также нельзя обращаться и из порожденных классов, а к protected переменным – можно. Т.о. класс CString3
аналогичным образом нельзя было породить из класса CString.
Хотя (в данном случае) можно было пойти `обходным’
путем:
class CString3_:
public CString
{
int SumLetters(){int
i,s=0; for(i=0;i>Len();i++)s+=GetStr()[i]; return s;}
};
В указанных моментах кроется повод для некоторых нареканий на язык С++: базовые классы следует очень тщательно проектировать. Если впоследствии нам потребуется получить доступ в порожденных классах к приватным переменным родительского класса, то напрямую мы его уже никак получить не сможем, не меняя, при этом, родительского класса.
При наследовании:
class CString3: public
CString2
…
вместо ключевого слова public можно было указать другие ключевые слова: private или protected. В данном случае указывается способ наследования переменных класса. При способе наследования public публичность переменных не изменяется. При способе наследования protected публичность переменных не изменяется, кроме public переменных, которые становятся protected. При способе наследования private все переменные класса становятся private.
Полиморфизм
Полиморфизмом называется способность языка использовать различные функции и операторы с одинаковыми именами. Какой вариант функции при этом используется – зависит либо от контекста, либо от внутренних свойств класса, для которого вызывается соответствующий метод.
Полиморфизм бывает трех типов:
·
Включения
·
Операционный
·
Параметрический
Полиморфизм включения
Существует две основных разновидности способов определения, какую функцию следует вызывать при выполнении программы в ответ на просьбу пользователя вызвать функцию с определенным именем.
При использовании первой разновидности способов конкретная функция определяется а этапе компиляции, исходя из информации, скрытой в самой программе. Данный подход носит название статического связывания.
При использовании второй разновидности способов конкретная функция определяется в процессе выполнения, исходя из информации, получаемой при выполнении кода. Данный подход носит название динамического связывания. Именно этот подход используется в языке С++ для реализации полиморфизма включения.
Рассмотрим
следующий пример
#include <stdio.h>
class CBase
{public:
virtual void
test(){printf("virtual check: CBase\n");}
void
test2(){printf("standard check: CBase\n");}
};
class CChild1:public CBase
{public:
void test(){printf("virtual
check: CChild1\n");}
void
test2(){printf("standard check: CChild1\n");}
};
class CChild2:public CBase
{public:
void test(){printf("virtual
check: CChild2\n");}
void
test2(){printf("standard check: CChild2\n");}
};
main()
{CBase *m[3]; int i;
m[0]=new CBase;
m[1]=new CChild1;
m[2]=new CChild2;
for(i=0;i<3;i++)m[i]->test();
for(i=0;i<3;i++)m[i]->test2();
return 0;
}
Функция test2 реализована в базовом классе CBase и в дочерних от него классах CChild1, CChild2. При вызове метода test2 для объекта типа CBase вызывается соответствующая функция из класса CBase , если же метод test2 вызывается для дочернего класса, то вызывается соответствующая функция дочернего класса. Информацию о том, какую функцию следует вызывать, легко получить на этапе компиляции из информации о типе соответствующего объекта. Т.о. здесь используется обычное статическое связывание.
Ситуацию можно изменить следующим образом. Пусть у нас есть указатель типа CBase*. Мы можем присвоить этому указателю указатель на объект типа CBase, а можем присвоить указатель на объект типа CChild1 или CChild2. С точки зрения функции test2 это не меняет ситуацию – она будет вызываться для базового класса в любом случае (если вы, конечно, не измените тип указателя). Однако, если перед описанием функции приписать ключевое слово virtual , то это приведет к тому, что при поиске требуемой функции будет использоваться динамическое связывание. В приведенном примере функция test базового класса является виртуальной. Поэтому в самом объекте хранится информация о том, какого типа данный объект. Для виртуальной функции информация о типе объекта берется не из информации о типе, которая есть у компилятора (в нашем примере переменная m[i] имеет тип CBase*, следовательно m[i] указывает на объект типа CBase), а из информации внутри самого класса. Поэтому после инициализации
m[1]=new CChild1();
в структуре, на которую указывает m[1] содержится информация о типе данного объекта. При вызове m[i]->test(); эта информация будет использована для того, чтобы вызвать функцию test из соответствующего порожденного класса CChild1.
В результате на экран будет выведено:
virtual check: CBase
virtual check: CChild1
virtual check: CChild2
standard check: CBase
standard check: CBase
standard check: CBase
Полиморфизм операционный. Перегрузка операторов и функций
Операционный полиморфизм использует механизм статического связывания. В языке в одном классе может быть несколько методов с одинаковыми именами, но разными параметрами. Подобный механизм называется механизмом перегрузки функций. Если используется механизм перегрузки функции, то для этой функции перестают действовать правила неявных преобразований типов для фактических параметров. При использовании перегрузки функций тип фактических параметров должен идеально совпадать с типом формальных параметров.
В реальности механизм перегрузки функций приводит к тому, что внутренне имя функции при компиляции программы состоит из собственно имени функции и из символов, задающих тип параметров функции. Это не соответствует способу внутреннего представления имен для языка С. Поэтому, вообще говоря, библиотечные функции, написанные на языке С (соответственно, при использовании компилятора с языка С) несовместимы с программами на языке С++. Ситуация решается введением ключевого слова `C’ (в разных компиляторах это слово может выглядеть несколько по-разному; например, в Microsoft Visual C++ для этих целей используется фраза extern "C"). С помощью данного ключевого слова можно указать компилятору, что внутренне имя для данной функции создавалось в соответствии с правилами языка С.
Переопределять можно не только функции, но и операторы. Например, определим класс для хранения комплексных чисел:
struct Complex{double re,im;};
Для этого класса (заметим, что класс мы определили как структуру) можно определить оператор сложения:
Complex operator+(Complex &x, Complex &y)
{Complex v; v.re=x.re+y.re; v.im=x.im+y.im; return v;}
Полиморфизм параметрический
Часто требуется использовать несколько одинаковых функций (или классов), отличающихся лишь типом параметров. Простейший пример: функции минимума, максимума, абсолютного значения и т.д. В языке С в этом случае можно применять оператор препроцессора define:
#define
MIN(x,y) ((x)<(y)?(x):y))
но это не всегда удобно, т.к. полноценная функция при этом не создается.
В языке С++
для этих целей используются шаблоны или
template:
template<class c> c min(c x,c y){return ((x)<(y)?(x):y));}
Фактически компилятор создает различные варианты этой функции для каждого варианта фактических параметров этой функции. Например, пусть эта функция вызвана следующим образом:
printf("%g %d %lg\n",min(3.f,4.f),min(3,4),min(3.,4.));
тогда компилятор создает три функции:
float min(float x, float y){return ((x)<(y)?(x):y));}
int min(int x, int y){return ((x)<(y)?(x):y));}
double min(double x, double y){return ((x)<(y)?(x):y));}
и вызывает их в
соответствующих местах программы.
Конструкторы и деструкторы*
Объекты рождаются и умирают. С этими событиями можно ассоциировать соответствующие функции: конструкторы и деструкторы. Конструктор автоматически вызывается в момент рождения объекта, а деструктор – в момент смерти.
Это очень удобно, т.к. дает возможность производить различные инициализации, с одной стороны, и очистку памяти после использования объекта, с другой.
Конструктором
считается функция, имеющая то же имя, что и имя класса. У деструктора то же
самое имя, но с символом `~’ перед именем функции. Например:
class CString
{
char *str; int l;
public:
CString(){l=256; str=new
char[l];}
CString(int l){this->l=l;
str=new char[l];}
~CString(){l=0; delete str;
str=NULL;}
};
CString s1,s2(1024);
Здесь мы создали две переменные. При создании первой переменной вызвался конструктор по умолчанию (без параметров), который отвел 256 ячеек памяти под строку. При создании второй переменой вызвался конструктор с целочисленным аргументом, который отвел 1024 ячеек памяти под строку. Память будет освобождена при смерти обеих переменных.
Конструкторы присваивания и копирования*
На самом
деле, надо хорошо понимать, что переопределение операций для сложных объектов
может быть весьма нетривиальной процедурой. Пусть объект требует нетривиальной
инициализации:
class CString
{
char *str; int l;
public:
CString(){l=256; str=new char[l];}
CString(int l){this->l=l; str=new char[l];}
~CString(){l=0; delete str; str=NULL;}
CString
& operator=(CString &from); //
об этом - далее
CString(CString &from); // об этом - далее
int Len(){return l;}
void Set(char *str)
{delete this->str; l=strlen(str);
this->str=new char[l+1]; strcpy(this->str,str);}
char *GetStr(){return str;}
};
В языке С++ можно передавать структуры (=классы) в функции и просто присваивать структуры друг другу. При этом происходит простое копирование структур:
CString s1,s2;
s2.Set(”String”); s1=s2;
Ясно, что подобные операции приведут к проблемам: при копировании s1=s2 память, предварительно выделенная в структуре s1, будет потеряна, а при смерти структур s1 и s2 будет почищена одна и та же память. В таких случаях следует переопределять оператор присваивания:
CString &CString::operator=(CString &from)
{
delete str; l=strlen(from.Len()); str=new
char[l+1];strcpy(str,from.GetStr());
return *this;
}
Если структура (=класс) передается в функцию по значению, то, по умолчанию, происходит ее простое копирование в структуру, являющуюся формальным параметром функции. При этом появляются те же проблемы с инициализацией и уничтожением внутренних объектов структуры. В таких случаях следует переопределять конструктор копирования, который будет автоматически вызываться в случаях, когда необходимо передать функцию в подпрограмму по значению:
CString:: CString (CString
&from)
{ l=strlen(from.Len()); str=new char[l+1];strcpy(str,from.GetStr());
}
Исключения*
Исключения, сами по себе, не имеют, практически, никакого отношения к объектно-ориентированному программированию. Они являются мощным средством отладки и повышения жизнеспособности программы. Надо понимать, что их использование в других сферах является идеологически неправильным.
Представим себе ситуацию, когда в процессе выполнения программы вы забрались глубоко в стек вызова процедур (т.е. из первой процедуры вызвана вторая, из второй третья, и т.д.). И тут обнаружилось, что данные, переданные в самую первую (исходную) процедуру оказались некорректными. В языке С ситуация решается возвратом соответствующего кода возврата из каждой вызванной процедуры. При этом, вы должны, естественно, после каждого вызова процедуры проверять ее код возврата и корректно его обрабатывать. Ясно, что далеко не всегда у программистов хватает сил на такую аккуратность.
В языке С++ ситуация решается с помощью исключений. Вызов самой первой процедуры помещается в блок, который ловит исключения. Внутри этого блока внутри любой вызванной процедуры можно выбросить исключение. После выбрасывания исключения код процедур перестает выполняться обычным образом, и программа просто последовательно выходит изо всех процедур, которые были вызваны, до того момента, пока не появится конец блока, который поймает данное исключение. Далее выполняется некоторый код, призванный обработать данное исключение, и далее восстанавливается обычный процесс выполнения программы.
К вышесказанному следует добавить, что после выбрасывания исключения, при выходе из процедур все же выполняются все необходимые деструкторы (что позволяет корректно освободить выделенные ресурсы).
Более формально: для выбрасывания исключения используется оператор throw. В качестве параметра ему выдается переменная некоторого типа T. Для ловли исключения используется следующий блок:
try{
…
}catch(T var){code};
здесь
T – тип переменной, которую выбросили в качестве исключения (т.о. ловятся только исключения, ассоциированные с переменными данного типа);
блок, в котором
происходит отлов исключений, размещается здесь на месте многоточия;
var – переменная типа T, которая получает значение выброшенной переменной, и которую можно использовать в произвольном куске пользовательского кода code.
Для отлавливания всех исключений вместо записи T var следует вписать многоточие. Например:
try{
int i=1,j=0;i=i/j;
}catch(…){printf(”Some problems\n”);};
Недостатки языка С++. Язык Java
Одним из
основных недостатков языка считается отсутствие двоичного стандарта языка.
Например, это выражается в несогласованности внутреннего представления функций.
Язык С++ допускает возможность перегрузки функций, а это требует, чтобы функции
с одинаковыми именами, но разными параметрами имели бы различное внутреннее
представление имен. Несмотря на наличие формального стандарта ISO/ANSI по внутреннему представлению имен функций, многие
производители ему не следует, что усложняет написание библиотек. В Windows эта проблема решается использованием DEF-файлов, сопоставляющих формальному имени функции ее
внутреннее имя.
Эта же проблема выступает при обработке исключений: исключения,
сгенерированные функциями, скомпилированными одним производителем, часто не могут
ловиться в функциях, скомпилированными другим производителем.
Язык С++
получил большое наследство языка С, в результате он получил сильную
привязанность кода к конкретной ЭВМ. Так, например, размер переменных
определенного типа зависит от используемой техники и, даже, от используемого
компилятора. Данный факт сильно усложняет переносимость программ.
Безусловной проблемой, унаследованной языком С++ от языка С, являются проблемы с отведением/освобождением памяти и, вообще, опасная работа с указателями.
Эти и многие другие проблемы были решены при создании языка программирования Java. В этом языке вообще нет указателей.
В языке существует несколько базовых типов:
|
Тип данных |
Размер занимаемой области памяти |
Значение по умолчанию |
|
boolean |
8 |
False |
|
byte |
8 |
0 |
|
char |
16 |
'x0' |
|
short |
16 |
0 |
|
int |
32 |
0 |
|
long |
64 |
0 |
|
float |
32 |
0.0F |
|
double |
64 |
0.0D |
Все эти типы имеют фиксированный размер, все они обязательно инициализируются по умолчанию. Все типы выполняют функции исключительно по смыслу им присущие. Т.е., например, переменная типа boolean может иметь только два значения: true и false. Эти значения не могут быть присвоены целым переменным. Аналогично, нельзя присвоить char переменную переменной типа int. Кстати, char переменные занимают 2 байта и используются для хранения символьных переменных в формате UNICODE (этот формат обеспечивает многоязыковую поддержку).
Базовые типы могут передаваться в функции только по значению (как в языке С). Зато все порожденные объекты (классы) передаются в функции только по ссылке. Более того, каждый объект любого класса используется как ссылка на объект. Т.е., например, прямое присваивание одного объекта другому является, всего лишь, присваиванием соответствующих ссылок (из чего следует, что ссылка, на которую ссылался объект, стоящий слева от знака присваивания, теряется). Для обычного присваивания содержимого объектов необходимо явно использовать соответствующие функции. Аналогично, при передаче объектов в функции, они передаются по ссылке.
Для каждого базового типа есть обертывающий класс – класс, содержащий всего одну переменную данного типа. Как и любой другой класс, обертывающие классы передаются в функции по ссылке. Например, создадим обертывающий класс для целой переменной:
Integer nSomeValue;
nSomeValue = new Integer(10);
В языке Java нельзя перегружать операторы. Поэтому все арифметические операции для обертывающих классов приходится выполнять с помощью явного вызова соответствующих функций.
Очистка памяти производится автоматически в процессе сборки мусора. При этом очищается память из-под объектов, на которые не осталось активных ссылок.
В языке Java наконец-то исключен из использования оператор goto. Подавляющее число случаев использования этого оператора связано с тем, что в программе может потребоваться выйти сразу из нескольких вложенных циклов. Выйти из одного цикла в языке С можно с помощью оператора break. В языке Java появился оператор break label, где label – метка, которая ставится перед оператором внешнего цикла, из которого следует выйти.
Упрощение
языка, по сравнению с С++, позволило не включать в язык Java
оператор typedef.
Операторов struct и union также нет в языке. Их роль легко могут играть классы.
Механизм определения классов очень похож на механизм С++:
class Point extends Object {
Point() {
x = 0.0;
y = 0.0;
}
Point(double
x, double y) {
this.x = x;
this.y = y;
}
public double
x;
public double
y;
}
В отличие от
С++, this является ссылкой на текущий объект, а не указателем
(указателей нет вообще). Все классы порождаются от одного класса Object.
Деструкторов в языке Java нет, но их роль может играть финализатор: метод с именем finalize:
protected void finalize() {
try {
file.close();
} catch
(Exception e) {
}
}
Лекция 11
Базовые принципы функционирования вычислительных систем
Список литературы
Вильям Столлингс. Операционные системы. Москва. Издательский дом ``Вильямс’’.
2002.
С.В.Зубков. Ассемблер для DOS, Windows и UNIX.
Михаил Гук. Аппаратные средства IBM PC.
Общая конфигурация вычислительной системы
Современная компьютерная система содержит центральный процессор, первичное и вторичное устройства хранения данных (память), устройства ввода и вывода, а также коммуникационные устройства (см. Рис. 1.1).
|
|
В современном компьютере можно выделить шесть основных компонентов.
Центральный процессор обрабатывает данные и управляет другими устройствами компьютера; первичная память хранит выполняющиеся в данный момент программы и обрабатываемые данные. Кроме центрального процессора в системе могут быть и дополнительные процессоры (сопроцессоры), играющие вспомогательные функции. Например, часто используются процессоры для непосредственной обработки вещественных чисел (плавающие процессоры). Кроме этого, возможны многопроцессорные конфигурации, когда в системе имеется несколько основных процессоров, которые распределяют между собой власть над памятью и устройствами.
Вторичная память хранит программы и данные для дальнейшего использования.
Устройства ввода преобразуют данные и инструкции в форму, удобную для обработки в компьютере.
Устройства вывода представляют информацию, обработанную компьютером, в виде, удобном для человеческого восприятия.
Коммуникационные устройства управляют приемом и передачей данных в локальных и глобальных сетях.
Устройства
ввода/вывода и коммуникационные устройства часто называются периферийными устройствами. Периферийные
устройства подключаются к компьютеру через внешние
интерфейсы с помощью адаптеров
или контроллеров, встроенных в
материнскую плату или в плату (карту) расширения. Адаптером называется средство сопряжения какого либо устройства с
шиной компьютера. Контроллером называется
практически то же самое, но предполагается, что он еще осуществляет некоторые
интеллектуальные функции. Часто контроллеры содержат свой внутренний
микропроцессор. Например, для непосредственного управления жесткими дисками
необходим контроллер диска. Для SCSI-дисков
контроллер размещается на материнской плате или на плате расширения, а для ATA/IDE-дисков контроллер размещается
непосредственно на самом диске.
Важным
контроллером, существенно ускоряющим некоторые операции ввода/вывода, является
контролер DMA (direct memory access). Данный контроллер управляет передачей данных
непосредственно между устройствами, что снижает нагрузку на CPU – центральный процессор. Например, для IDE-дисков существует режим работы UDMA,
предусматривающий прямой обмен данными между диском и памятью. Стандартный
обмен осуществляется в режиме PIO. Режим UDMA не просто повышает пропускную способность канала, он
гарантирует данную пропускную способность, независимо от загруженности CPU, чего нет в режиме PIO.
Алгоритм обмена процессора с винчестером
таков: центральный процессор
инициирует операцию чтения; винчестер считывает первый сектор в буфер и выдает
прерывание, продолжая читать следующие секторы; процессор либо забирает данные
из буфера по протоколу PIO, либо это делает сам контроллер винчестера по протоколу
DMA; процесс повторяется до передачи последнего сектора. Основное отличие режимов DMA
и PIO не в
скорости передачи данных, а в том, что в интервалах между получением данных в
режиме PIO CPU остается занятым, а в режиме DMA – он может
вести дополнительную работу. Это важно, например, при обработке потокового
видео, когда требуются весьма большие вычислительные ресурсы.
Центральный
процессор преобразует поток данных в удобную для обработки форму, а также
управляет другими компонентами компьютерной системы. Первичное хранилище данных
временно хранит инструкции программы и данные во время обработки. Вторичное
устройство хранения данных (магнитный или лазерный диск, магнитная лента)
хранит данные и программы, которые не участвуют в обработке в данный момент.
Устройства ввода, такие как клавиатура и мышь, преобразуют данные и команды в
электронную форму, понятную компьютеру. Устройства вывода, такие как принтер и
монитор, преобразуют электронные данные, представленные компьютером, и
отображают их в той форме, в какой их могут понять люди. Коммуникационные
устройства обеспечивают соединения между компьютерами и компьютерными сетями. Шина
(bus) – это устройство для передачи данных и сигналов между различными
частями компьютерной системы.
Системные шины на IBM PC – совместимых комьютерах.
ISA (Industrial Standard Architecture) – старый формат шины. ISA это - общая шина, то есть все устройства компьютера, сидящие на этой шине, выстраиваются в общую очередь на обслуживание. Разрядность адреса - 16 бит, разрядность данных - 8 бит (для XT) и 8/16 бит (для AT). Тактовая частота - 8 МГц (для XT). Для AT - обычно равна внешней тактовой частоте процессора.
Основные отличия шины ISA персонального компьютера IBM PC/AT от своей предшественницы - шины компьютера IBM PC/XT заключаются в следующем:
- шина AT компьютеров позволяет использовать на внешних платах как 16-разрядные устройства ввода/вывода, так и 16-разрядную память;
- цикл доступа к 16-разрядной памяти на внешней плате может быть выполнен без вставки тактов ожидания;
- объем непосредственно адресуемой памяти на внешних платах может достигать 16 Мб;
- внешняя плата может становиться хозяином (задатчиком) на шине и самостоятельно осуществлять доступ ко всем ресурсам как на шине, так и на материнской плате.
К настоящему времени ISA морально устарела и является тормозом для развития материнских плат. Однако полностью отказаться от нее пока не удается, так как до сих пор эксплуатируются платы расширения на шине ISA - например, модемы и звуковые карты.
PCI (Peripheral Component Interconnect bus) - шина для подключения периферийных компонентов, независимая от платформы. Впервые появилась в 1992 г. на PC с процессором 486. Частота шины от 20 до 33 МГц, теоретически максимальная скорость 132/264 Мбайт/с для 32/64 бит. В современных материнских платах частота на шине PCI задается как 1/2 входной частоты процессора, т.е при частоте 66 MHz на PCI будет 33 MHz, при 75 MHz - 37.5 MHz. Каждый слот PCI - отдельная шина, конфигурация которой задается в BIOS.
Строго говоря, шина PCI не является локальной, т.к. между ней и шиной процессора имеется специальный, согласующий сигналы блок. Кроме этого, стандарт PCI предусматривает использование вспомогательного контроллера, который берет на себя разделение сигналов процессора и шины и осуществляет разрешение конфликтов. Таким образом, шина PCI является независимой от типа процессора.
Bus
mastering (Управление шиной)
Bus mastering (Управление шиной) это функция шины PCI которая может использоваться
любым PCI устройством (например контроллером диска, графическим контроллером
или звуковой картой). Bus mastering позволяет устройству управлять шиной и
осуществлять (инициировать) любые транзакции чтения / записи к другим
устройствам на шине PCI или к системной памяти. Эти транзакции осуществляются
независимо от главного процессора, поэтому они отнимают время только у шины, но
не у процессора. Bus mastering транзакции не быстрее обычных транзакций,
осуществляемых процессором. Преимущество bus mastering в том, что контроллер
запрограммированный на выполнение какой-либо передачи данных или на выполнение
последовательности команд больше не требует действий от процессора пока он
(контроллер) не завершит свою задачу. Обычно для информирования процессора о
том, что хозяин шины (bus master) выполнил свои действия используется механизм
прерываний.
В случае с графическими контроллерами, PCI bus mastering используется для двух
важных назначений:
Передача данных о изображении из системной памяти в видео память - это может включать передачу изображений и текстур которые будут использованы в будущей генерации изображения.
Считывание графических команд ("список показа") из системной памяти. В этом случае процессор (под управлением графического драйвера) подготавливает последовательность командных примитивов и помещает их где-либо в системной памяти. Затем посылаются команды графическому контроллеру, которые предписывают ему принять и выполнить последовательность команд начиная с данного адреса в системной памяти. Процессор может работать над следующей сценой, в то время как текущая сцена отрисовывается графическим контроллером.
AGP
В основном AGP (Accelerated Graphics Port) это вариант PCI, поэтому все
операции контроллеров AGP интерфейса обладают всеми возможностями PCI
устройств. Оба интерфейса 32 битной ширины и большинство сигналов одинаковы. В
PCI много слотов, в то время как AGP - поточечное соединение. PCI работает с
частотой 33 МГц, AGP - 66 МГц. AGP интерфейс может производить два типа
транзакций: PCI транзакции и AGP транзакции. Единственные AGP транзакции
являются "bus mastering" передачами из системной памяти графическому
контроллеру и инициируются графическим контроллером. Все остальные транзакции
производятся как PCI передачи. Даже при этом эти транзакции вдвое быстрее чем
транзакции на PCI шине из-за более высокой тактовой частоты AGP интерфейса.
Некоторые старые AGP-карты могут производить только PCI-транзакции.
Предположительно примерами таких "быстрых PCI" карт могут быть Matrox
Millenium II AGP и Trident 9650.
Чем AGP отличается от PCI?
|
AGP |
PCI |
|
Конвейерная
организация |
Не
конвейерная организация. |
|
Разделение
каналов адресации и транзакции |
Одновременно
|
|
Максимум 533Mб/с
32 бита |
Максимум 133Mб/с
32 бита |
|
Одно
назначение |
Мультиназначение
|
|
Только
операции записи/чтения памяти, никаких других операций ввода вывода. |
Канал
ко всей системе |
AGP
транзакции - адресация по побочной частоте
AGP транзакции используются только в "bus mastering" режиме. В то
время как в простых PCI транзакциях при быстрейшей транзакции может
передаваться 4 32-битных слова за 5 тактов часов (так как кроме данных надо еще
передать адрес – куда их поместить), AGP передачи могут использовать
дополнительные AGP линии называемые Побочными (Sideband) для передачи адреса
маленькими кусочками одновременно с данными. Во время передачи пакета из 4 слов
передаются 4 части адреса для следующего пакетного (взрывного) цикла. По
завершении цикла адрес и информация запроса для следующего пакета уже переданы,
поэтому следующий 4-словный пакет может начинать сразу же передаваться. Таким
образом, мы можем передать 4 слова за 4 цикла (а не за 5, необходимые PCI).
Вместе с 66 МГц частотой часов это предоставляет максимальную скорость передачи
(4x66=) 264 МБайт/с.
Помимо более быстрых часов, AGP интерфейс обладает другими опциями которые
могут увеличить скорость передачи данных. Во время осуществления
AGP-транзакций, интерфейс может работать в одном из четырех режимов, отмечаемых
как 1x, 2x, 4x и 8x.
Действительный режим, используемый для AGP передачи, устанавливается между
материнской платой и AGP картой во время системной инициализации, и после его
определения остается неизменным. Установка режима зависит от доступности /
поддержки конкретного режима и его стабильности. Вот почему многие потенциально
2х совместимые системы работают только как 1х - это случается если драйвер
определяет, что 2х режим может привести к ошибкам передачи.
1x режим передает одну порцию (слово) данных и побочную информацию при каждом такте часов. Это приносит 264 МБ/с.
2x режим передает данные и побочную информацию в начале и конце каждого такта часов, поэтому две порции данных передаются за один такт часов, при этом общий максимальный вывод соответствует 528 МГц.
В 4x режиме тактовая частота остается равной 66 МГц, но два других сигнала, запускающиеся синхронно с главными часами с эффективной частотой 133 МГц, используются для передачи данных в начале и конце каждого такта. Это приносит максимальный вывод свыше 1 Гб/с.
Прерывания
Процесс выполнения программы сводится, в конечном счете, к следующему. Программа
представляет собой набор последовательно записанных команд. Как правило,
существует регистр, в котором хранится номер текущий команды. Элементарный шаг
выполнения программы называется циклом.
В процессе исполнения цикла происходит выборка
команды и исполнение команды.
Сразу после выборки команды счетчик команд увеличивается так, что он указывает
на следующую команду.
Базовым понятием при описании принципов действия ЭВМ является прерывание. Бывают прерывания четырех типов:
Программные прерывания
Аппаратные прерывания
Прерывания ввода/вывода
Прерывания по таймеру
При исполнении прерывания происходит приостановка выполнения основной программы, данные о адресе текущей команды (регистр с адресом текущей команды) и состояние системы (например, регистр флагов) сохраняются (как правило, в стек) и происходит передача управления на программу обработки прерывания. После ее завершения состояние системы восстанавливается, и управление передается на прерванную команду. Отметим, что часто перед обработкой прерывания приходится сохранять гораздо больше данных. Например, обычно сохраняются значения всех регистров. Но это уже - забота функции обработки прерывания.
Очевидно, что прерывание не может наступать в произвольный момент. Поэтому в цикл выполнения программы добавляется еще один этап: проверка наличия прерывания. Именно на этом этапе будет возможен вызов прерывания. Если его поместить после этапа исполнения команды, то в стеке надо будет сохранить текущий регистр с адресом исполняемой команды (он увеличился сразу после выборки команды), а после завершения прерывания надо вернуться по этому адресу.
В процессе выполнения некоторых прерываний следует запретить вызов других прерываний. Этот процесс называется блокировкой вызовов прерываний. Вызов прерываний всегда блокируется при, собственно, вызове прерывания, когда необходимые данные загружаются в стек и происходит переход к процедуре исполнения прерывания.
Часто прерывания реализуются с помощью таблицы прерываний. Таблица прерываний представляет собой массив, в каждой ячейке которой хранится адрес процедуры обработки прерывания и, возможно, некоторая дополнительная информация. В этом случае каждое прерывание ассоциируется с некоторым номером n и вызов прерывания n ассоциируется с вызовом процедуры обработки прерывания, адрес которой находится в ячейке таблицы прерываний n.
Прерывания очень полезны, например, для обработки операций ввода/вывода. Эти операции весьма медлительны, поэтому было бы разумным (на самом деле так происходит далеко не всегда) запустить эту процедуру и вернуть управление текущей программе. Далее, когда от процессора будет требоваться вмешательство в процесс ввода/вывода (например, данные попали, наконец, в буфер ввода/вывода), то вызовется прерывание, которое обработает эти данные и вернет управление текущей программе.
Кэш-память
Cache (запас) обозначает
быстродействующую буферную память между процессором и основной памятью. Кэш
служит для частичной компенсации разницы в скорости процессора и основной
памяти - туда попадают наиболее часто используемые данные. Когда процессор
первый раз обращается к ячейке памяти, ее содержимое параллельно копируется в
кэш, и в случае повторного обращения в скором времени может быть с гораздо
большей скоростью выбрано из кэша. При записи в память значение попадает в кэш,
и либо одновременно копируется в память (схема Write Through - прямая или сквозная запись), либо копируется через
некоторое время (схема Write Back -
отложенная или обратная запись). При обычной обратной записи, называемой также буферизованной сквозной записью,
значение копируется в память в первом же свободном такте, а при отложенной (Delayed Write) - когда для помещения в кэш нового значения не
оказывается свободной области; при этом в память вытесняются наименее
используемая область кэша. Вторая схема более эффективна, но и более сложна за
счет необходимости поддержания соответствия содержимого кэша и основной памяти.
Сейчас под термином Write Back в основном понимается отложенная запись, однако это может означать и буферизованную сквозную.
Сквозная запись имеет существенный недостаток: при выполнении подряд идущих операций записи в память кеш, практически, отключается и скорость записи определяется только скоростью работы основной памяти. С другой стороны, в многопроцессорных системах данный подход обеспечивает согласованность оперативной памяти: данные, записанные различными процессорами, оказываются сразу же в памяти. Однако, при этом кэш может оказаться несогласованным с памятью: один процессор может не знать о том, что другой записал что-то в память. В этом случае необходим цикл просмотра памяти для согласования памяти и кеша. Отметим, что в реальных системах операций чтения памяти гораздо больше операций записи (например, при обращении к командам используются вообще только операции чтения). Реально, примерно 10% операций являются операциями записи, а остальные – операциями чтения.
При использовании отложенной записи запись в память осуществляется или при вытеснении данных из Кеша или при особых событиях. Например, в Pentium-компьютерах это может осуществиться даже программным путем с помощью посылки специальной команды или с помощью аппаратного сигнала. Ясно, что смена строк Кеш-памяти для случая отложенной записи требует больше времени, чем в случае сквозной Кеш-памяти, т.к. перед записью строки в Кеш необходимо еще вытеснить текущую строку Кеша в память.
При записи в память при возникновении промахов (т.е. ситуаций, когда данные по записываемому адресу не размещены в Кеше) возможно использование двух стратегий: стратегия с размещением и стратегия без размещения. При использовании стратегии с размещением данные параллельно записываются и в Кеш и в память. На самом деле, обычно, сначала процессор записывает данные в основную память и продолжает свою работу, а Кеш-контроллер параллельно считывает соответствующую Кеш-строку из памяти в Кеш. Данная стратегия имеет очень сложную реализацию, поэтому часто при записи данных Кеш-память просто игнорируется (=стратегия без размещения).
Память для кэша состоит из собственно области данных, разбитой на блоки (строки), которые являются элементарными единицами информации при работе кэша, и области признаков (tag), описывающей состояние строк (свободна, занята, помечена для дозаписи и т.п.). В основном используются две схемы организации кэша: с прямым отображением (direct mapped), когда каждый адрес памяти может кэшироваться только одной строкой (в этом случае номер строки определяется младшими разрядами адреса), и n-связный ассоциативный (n-way associative), когда каждый адрес может кэшироваться несколькими строками. Ассоциативный кэш более сложен, однако позволяет более гибко кэшировать данные; наиболее распространены 4-связные системы кэширования.
Процессоры 486 и выше имеют также внутренний (Internal) кэш объемом 8-16 кб. Он также обозначается как Primary (первичный) или L1 (Level 1 - первый уровень) в отличие от внешнего (External), расположенного на плате и обозначаемого Secondary (вторичный) или L2. В большинстве процессоров внутренний кэш работает по схеме с прямой записью, а в Pentium и новых 486 (Intel P24D и последние DX4-100, AMD DX4-120, 5x86) он может работать и с отложенной записью. Последнее требует специальной поддержки со стороны системной платы, чтобы при обмене по DMA можно было поддерживать согласованность данных в памяти и внутреннем кэше. Процессоры Pentium Pro имеют также встроенный кэш второго уровня объемом 256 или 512 кб. Кеш L1 работает на частоте процессора, Кеш L2 работает на частоте шины. Т.о., используется то, что частота шины выше частоты, с которой происходит выемка из памяти, а частота процессора выше частоты шины. Например, в самых современных процессорах поддерживается тактовая частота 3.2 ГГц, частота шины 800МГц, а самая совершенная память для PIV поддерживает частоту 400 МГц (отметим, что данные частоты могут указывать не настоящие частоты, а частоты, на которых происходит передача данных: за один такт может передаваться две порции данных).
В платах 386 чаще всего использовался внешний кэш объемом 128 кб, для 486 - 128..256 кб, для Pentium - 256..512 кб.
Организация Кеш-памяти и ассоциативная память в IBM PC-совместимых ЭВМ
Рассмотрим пример процессора i386, имеющего 16K ассоциативной Кеш-памяти. Для ее реализации используется быстрая (и дорогая) SRAM-память. Кеш-строка содержит 16 байт.
Внутри Кеш-контроллера 32-битный адрес делится на три части:
· Биты B31-B12 (20 бит) - адрес дескриптора
· Биты B11-B4 (8 бит) - адрес набора
· Биты B3-B2 (2 бит) - адрес слова (имеются в виду 4-байтные слова).
Т.о. для адреса x имеем:
D(x)=((x>>12)&((1<<20)-1)) номер
дескриптора
S(x)=((x>>4)&((1<<8)-1)) номер набора
W(x)=((x>>2)&3) номер слова
B(x)=(x&3) номер
байта
Ячейка Кеш-блока состоит из Кеш-директории и, собственно, Кеш-записи.
Кеш-директория содержит 20 бит со значением дескриптора данной Кеш-записи и 5 бит признаков: бит защиты, бит занятости, 3 бита LRU (об этом – позже).
Бит защиты предохраняет Кеш-запись от изменения и считывания в процессе цикла записи Кеш-строки. Во время цикла записи он устанавливается равным 1, а в остальное время он равен 0.
Бит занятости указывает, на то, что данная Кеш-строка реально отражает содержимое общей памяти. Например, при изменении памяти в режиме DMA данный бит должен быть обнулен. Если данные в Кеше соответствуют данным в основной памяти, то данный бит должен быть равным 1.
Отметим, что когда мы говорили о 16K памяти, то имели в виду лишь память, в которой будут храниться непосредственно данные. Реально еще необходима память для хранения Кеш-директорий. Более того, последняя память будет более часто использоваться и должна иметь большее быстродействие.
Вся Кеш память разбивается на магистрали. В нашем случае используется
4 магистрали. Каждая магистраль состоит из массива строк по 16 байт. Для данного адреса x внутри
магистрали однозначно задается номер соответствующего набора = S(x). Т.о., размер
магистрали равен длине строки умножить на количество наборов = 28*24=4K, а т.к. у нас всего
4 магистрали, то размер всей Кеш-памяти равен 16K.
Если требуется внести в Кеш ячейку памяти с адресом x, то это можно сделать только вместе со всей строкой в памяти, содержащей x. Итак, пусть требуется внести в память строку, соответствующую адресу x. Мы сразу можем посчитать номер набора для этой строки = S(x). Этот набор может быть расположен в одной из четырех магистралей в наборе с номером S(x), поэтому мы должны сравнить D(x) со значениями дескрипторов в Кеш-директориях с номерами изо всех магистралей, где в данных Кеш-директориях бит защиты = 0 и бит занятости = 1.
Если нашелся дескриптор, равный
дескриптору вносимой строки, то считается, что произошло Кеш-попадание и данные
могут быть внесены в соответствующую Кеш-строку. Иначе, произошел Кеш-промах.
Если среди Кеш директорий с номером S(x) нашлась свободная директория (т.е. значение ее бита
занятости = 0), то мы можем разместить свои данные в соответствующей
Кеш-записи. Иначе нам придется выбрать одну из занятых Кеш-записей с номером S(x), вытеснить ее в
обычную память и занести нашу Кеш-строку на ее место, модифицировав значения
дескриптора в Кеш-директории на значение D(x).
Простейшая стратегия выбора подходящей магистрали – выбор ее случайным образом. Возможен более аккуратный способ, когда выбирается давно использующаяся Кеш-запись. Это делается с помощью LRU-бит в Кеш-директории. Например, это можно сделать следующим способом. Обозначим биты LRU: B0, B1, B2.
Если произошел доступ к магистрали 0 или 1, то установим B0=1, при этом если произошел доступ к магистрали 0, то установим B1=0, иначе установим B1=1.
Если произошел доступ к магистрали 2 или 3, то установим B0=0, при этом если произошел доступ к магистрали 2, то установим B2=0, иначе установим B2=1.
Т.о. образом, бит B0 указывает, к какой паре магистралей произошел последний доступ. Т.е. если B0==0, то использовать для замещения нужно магистрали 0 или 1, а если если B0==1, то использовать для замещения нужно магистрали 2 или 3. Оставшиеся биты указывают, какая из двух магистралей использовалась последней. Т.е. если B0==0&& B1==0, то последней из двух магистралей 0 и 1 использовалась магистраль 0, поэтому для замещения надо использовать магистраль 1.
Если B0==0&& B1==1, то последней из двух магистралей 0 и 1 использовалась магистраль 1, поэтому для замещения надо использовать магистраль 0.
Если B0==1&& B2==0, то последней из двух магистралей 2 и 3 использовалась магистраль 2, поэтому для замещения надо использовать магистраль 3.
Если B0==1&& B2==1, то последней из двух магистралей 2 и 3 использовалась магистраль 3, поэтому для замещения надо использовать магистраль 2.
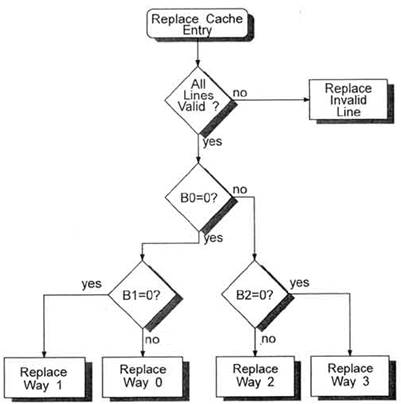
На практике оказывается, что стратегия случайного замещения Кеш-записей оказывается не намного хуже стратегии LRU.
Режимы адресации памяти в Intel-процессорах
Можно говорить о трех основных режимах, в которых может находится процессор Intel: реальный режим, V86 режим, защищенный режим. Подобное разнообразие режимов является не преимуществом данного процессора, а следствием тяжелого требования совместимости со старыми операционными системами и старым программным обеспечением.
Реальный режим
В него попадает компьютер сразу после включения питания.
Регистры общего назначения
32-битные регистры:
EAX аккумулятор (используется для помещения результата некоторых операций; в данный регистр помещается младшая часть результата, а в EDX-старшая)
EBX база (для адресации по базе)
ECX счетчик (для циклов)
EDX регистр данных
К младшей паре байт этих
регистров можно обращаться как к регистрам AX, BX, CX, DX. Более того, к младшим байтам этих
регистров можно обращаться как к AL, BL, CL, DL, а ко второму из двух байт, как к
регистрам AH, BH, CH, DH.
Сегментные регистры и регистры стека
В реальном режиме адрес может быть записан в виде 16-битных адресов сегмента и смещения внутри сегмента. Адрес сегмента записывается с 4-битным смещением (т.е. адрес, деленный на 16). Т.о. всего можно обратиться к 220 ячейкам памяти = 1М.
В процессорах Intel предусмотрено шесть шестнадцатибитных регистров — CS, DS, ES, FS, GS, SS, используемых для хранения селекторов. CS используется для указания сегмента кода. 16-битные регистры CS и EIP используются для указания адреса следующей исполняемой инструкции. Т.о. команда перехода эквивалентна простому изменению этих регистров.
SS используется для указания сегмента стека. Вершина стека указывается регистром ESP. Отметим, что стек растет в сторону меньших адресов, что удобно, если у нас все сегменты используют одну область памяти. Тогда переменные программы могут размещаться в нижней области памяти, а стек – в верхней.
Остальные регистры (DS, ES, FS, GS) используются для сегментов данных.
Регистр флагов EFLAGS
Используется процессором, для пометки различных ситуаций. Каждый бит данного флага помечает отдельную ситуацию: переполнение в последней команде, равенство нулю результата последней команды, и т.д.
Регистры для работы с плавающей точкой
Регистры данных (R0 – R7) не адресуются по именам, а представляют собой
стек, куда можно загружать данные, осуществлять операции над вершиной стека,
извлекать данные из стека.
Защищенный режим
Данный режим намного более сложнее предыдущего. Он позволяет адресовываться к 4G памяти.
В данном режиме также присутствуют сегменты, но адрес сегмента задается сложнее. Адрес сегмента задается с помощью 16-битных регистров, называемых селекторами. Селектор указывает не адрес начала сегмента, а номер в специальной таблице дескрипторов, в которой содержится адрес начала сегмента. Более конкретно, селектор имеет следующий вид:
биты 15 – 3: номер дескриптора в таблице
бит 2: индикатор таблицы 0/1 — использовать GDT/LDT
биты 1 – 0: уровень привилегий запроса (RPL)
Существует одна глобальная таблица дескрипторов (GDT) и по одной таблице на каждую задачу (LDT). Таблица дескрипторов состоит из 8-байтных полей, содержащих довольно много информации. Нам интересны:
База сегмента 32-битный регистр
Лимит сегмента 20-битнй регистр
Бит гранулярности
База сегмента задает адрес начала
сегмента. Лимит сегмента задает максимальный размер сегмента в байтах, если бит
гранулярности=0, или максимальный размер сегмента в блоках по 4096 байт, если
бит гранулярности=1. Т.о., максимальный размер сегмента может быть 4G.
Своему названию данный режим обязан широким возможностям за отслеживанием корректности обращения к данным. Так, например, обращение за пределы сегмента приводит к исключению. В дескрипторе задается тип сегмента: код или данные и права обращения к сегменту: для сегмента данных – право записи, для сегмента кода – право на чтение. В селекторе задается одна из четырех привилегий по работе с сегментом. Максимальная привилегия (=0) дается системных задачам, минимальная (=3) – пользовательским. При этом, если программа имеет более высокие привилегии, то при обращении к данному сегменту они понизятся до привилегия сегмента.
Страничная организация памяти в защищенном режиме
При его реализации память разбивается на страница по 4K. Каталог страниц занимает одну страницу и содержит 1024 4-байтных адресов обычных таблиц страниц. Каждая таблица страницы располагается в отдельной странице. Обычный 32-битный адрес представляется следующим образом. Биты 31-22 дают номер записи в каталоге страниц. Следующие 10 бит с номерами 21-11 дают номер записи в таблице страниц, на которую ссылается соответствующая запись в каталоге страниц. И, наконец, последние младшие 12 бит дают смещение внутри страницы. Данная адресация абсолютно прозрачна на пользовательском уровне.
Для ускорения процедуры используется специальный Кеш страниц TLB.
В каждой записи в таблице страниц для задания адреса страницы используется 20 бит, а в остальных 12 содержится много дополнительной информации. Например, там есть бит, указывающий – существует ли реально в памяти данная страница. Это дает возможность вызывать соответствующее прерывание при обращении к странице, которой нет в памяти. В современных операционных системах данное прерывание используется для поддержки виртуальной памяти. Оно скачивает требуемую страницу с диска (из файла подкачки), корректно устанавливает значения в соответствующей записи в таблице дескрипторов, возможно, вытесняет некоторую страницу на диск и возвращает управление в текущую программу.
Лекция 12
Базовые принципы функционирования вычислительных систем
Список литературы
Вильям Столлингс. Операционные системы. Москва. Издательский дом ``Вильямс’’.
2002.
С.В.Зубков. Ассемблер для DOS, Windows и UNIX.
Михаил Гук. Аппаратные средства IBM PC.
Режимы адресации памяти в Intel-процессорах
Можно говорить о трех основных режимах, в которых может находится процессор Intel: реальный режим, V86 режим, защищенный режим. Подобное разнообразие режимов является не преимуществом данного процессора, а следствием тяжелого требования совместимости со старыми операционными системами и старым программным обеспечением.
Реальный режим
В него попадает компьютер сразу после включения питания.
Регистры общего назначения
32-битные регистры:
EAX аккумулятор (используется для помещения результата некоторых операций; в данный регистр помещается младшая часть результата, а в EDX-старшая)
EBX база (для адресации по базе)
ECX счетчик (для циклов)
EDX регистр данных
К младшей паре байт этих
регистров можно обращаться как к регистрам AX, BX, CX, DX. Более того, к младшим байтам этих
регистров можно обращаться как к AL, BL, CL, DL, а ко второму из двух байт, как к
регистрам AH, BH, CH, DH.
Сегментные регистры и регистры стека
В реальном режиме адрес может быть записан в виде 16-битных адресов сегмента и смещения внутри сегмента. Адрес сегмента записывается с 4-битным смещением (т.е. адрес, деленный на 16). Т.о. всего можно обратиться к 220 ячейкам памяти = 1М.
В процессорах Intel предусмотрено шесть шестнадцатибитных регистров — CS, DS, ES, FS, GS, SS, используемых для хранения селекторов. CS используется для указания сегмента кода. 16-битный регистр CS и 32/16 битный регистр EIP/IP используются для указания адреса следующей исполняемой инструкции. Т.о. команда перехода эквивалентна простому изменению этих регистров.
SS используется для указания сегмента стека. Вершина стека указывается регистром ESP. Отметим, что стек растет в сторону меньших адресов, что удобно, если у нас все сегменты используют одну область памяти. Тогда переменные программы могут размещаться в нижней области памяти, а стек – в верхней.
Остальные регистры (DS, ES, FS, GS) используются для сегментов данных.
Регистр флагов EFLAGS
Используется процессором, для пометки различных ситуаций. Каждый бит данного флага помечает отдельную ситуацию: переполнение в последней команде, равенство нулю результата последней команды, и т.д.
Регистры для работы с плавающей точкой
Регистры данных (R0 – R7) не адресуются по именам, а представляют собой
стек, куда можно загружать данные, осуществлять операции над вершиной стека,
извлекать данные из стека.
Защищенный режим
Данный режим намного более сложнее предыдущего. Он позволяет адресовываться к 4G памяти.
В данном режиме также присутствуют сегменты, но адрес сегмента задается сложнее. Адрес сегмента задается с помощью 16-битных регистров, называемых селекторами. Селектор указывает не адрес начала сегмента, а номер в специальной таблице дескрипторов, в которой содержится адрес начала сегмента. Более конкретно, селектор имеет следующий вид:
биты 15 – 3: номер дескриптора в таблице
бит 2: индикатор таблицы 0/1 — использовать GDT/LDT
биты 1 – 0: уровень привилегий запроса (RPL)
Существует одна глобальная таблица дескрипторов (GDT) и по одной таблице на каждую задачу (LDT). Таблица дескрипторов состоит из 8-байтных полей, содержащих довольно много информации. Нам интересны:
База сегмента 32-битный регистр
Лимит сегмента 20-битнй регистр
Бит гранулярности
База сегмента задает адрес начала
сегмента. Лимит сегмента задает максимальный размер сегмента в байтах, если бит
гранулярности=0, или максимальный размер сегмента в блоках по 4096 байт, если
бит гранулярности=1. Т.о., максимальный размер сегмента может быть 4G.
Своему названию данный режим обязан широким возможностям за отслеживанием корректности обращения к данным. Так, например, обращение за пределы сегмента приводит к исключению. В дескрипторе задается тип сегмента: код или данные и права обращения к сегменту: для сегмента данных – право записи, для сегмента кода – право на чтение. В селекторе задается одна из четырех привилегий по работе с сегментом. Максимальная привилегия (=0) дается системных задачам, минимальная (=3) – пользовательским. При этом, если программа имеет более высокие привилегии, то при обращении к данному сегменту они понизятся до привилегия сегмента.
Страничная организация памяти в защищенном режиме
При его реализации память разбивается на страница по 4K. Каталог страниц занимает одну страницу и содержит 1024 4-байтных адресов обычных таблиц страниц. Каждая таблица страницы располагается в отдельной странице. Обычный 32-битный адрес представляется следующим образом. Биты 31-22 дают номер записи в каталоге страниц. Следующие 10 бит с номерами 21-11 дают номер записи в таблице страниц, на которую ссылается соответствующая запись в каталоге страниц. И, наконец, последние младшие 12 бит дают смещение внутри страницы. Данная адресация абсолютно прозрачна на пользовательском уровне.
Для ускорения процедуры используется специальный Кеш страниц TLB.
В каждой записи в таблице страниц
для задания адреса страницы используется 20 бит, а в остальных 12 содержится
много дополнительной информации. Например, там есть бит, указывающий –
существует ли реально в памяти данная страница. Это дает возможность вызывать
соответствующее прерывание при обращении к странице, которой нет в памяти. В
современных операционных системах данное прерывание используется для поддержки
виртуальной памяти. Оно скачивает требуемую страницу с диска (из файла
подкачки), корректно устанавливает значения в соответствующей записи в таблице
дескрипторов, возможно, вытесняет некоторую страницу на диск и возвращает
управление в текущую программу.
Операционные системы
Операционная Система - это программа, контролирующая работу прикладных и системных приложений и исполняющая роль интерфейса между пользователем и аппаратным обеспечением компьютера.
Данное определение весьма условно. На данный момент сложилось некоторое общее представление о том, что должна делать ОС. Это представление зафиксировано в стандарте POSIX (Portable OS Interface based on uniX) и при разработке новых ОС всегда происходит оглядка на данный стандарт.
Определить место ОС во всей вычислительной системе можно из следующей картинки, определяющей уровни вычислительной системы и различные точки зрения на нее:
![]()
![]()
По современным представлениям, ОС должна уметь делать следующее:
- Обеспечивать загрузку пользовательских программ в оперативную память и их исполнение.
- Обеспечивать работу с устройствами долговременной памяти, такими как магнитные диски, ленты, оптические диски и т.д. Как правило, ОС управляет свободным пространством на этих носителях и структурирует пользовательские данные.
- Предоставлять более или менее стандартный доступ к различным устройствам ввода/вывода, таким как терминалы, модемы, печатающие устройства.
- Предоставлять некоторый пользовательский интерфейс. Слово некоторый здесь сказано не случайно - часть систем ограничивается командной строкой, в то время как другие на 90% состоят из средств интерфейса пользователя.
Существуют ОС, функции которых этим и исчерпываются. Одна из хорошо известных систем такого типа - дисковая операционная система MS DOS.
Более развитые ОС предоставляют также следующие возможности:
- Параллельное (точнее, псевдопараллельное, если машина имеет только один процессор) исполнение нескольких задач.
- Распределение ресурсов компьютера между задачами.
- Организация взаимодействия задач друг с другом.
- Взаимодействие пользовательских программ с нестандартными внешними устройствами.
- Организация межмашинного взаимодействия и разделения ресурсов.
- Защита системных ресурсов, данных и программ пользователя, исполняющихся процессов и самой себя от ошибочных и зловредных действий пользователей и их программ.
В силу вышесказанного можно провести грубую классификацию операционных систем:
Дисковые операционные системы. ДОС. Это системы, берущие на себя только первые четыре функции. Классический пример – MS DOS. Система по определению может работать только с одной задачей (если не рассматривать недокументированные возможности). После загрузки задачи полный контроль над системой передается задаче и ОС, практически, никак не может помешать задаче сделать с системой что угодно – например, порушить саму ОС. Если пользовательская программа была абсолютно корректной, то после ее завершения управление системой передается опять ОС и она продолжает интерфейс с пользователем.
Безусловно, не стоит недооценивать ОС MS DOS. В ней можно найти много красивых идей, украденных у UNIX, например, в ней существуют подобия файлов устройств (например, PRN, NUL, CON), понятие стандартных потоков ввода вывода, перенаправления в стандартные потоки ввода/вывода/вывода сообщений об ошибках (в точности так же, как и в UNIX). Существует понятие конвейера. Хотя задачи в конвейере (в силу однозадачности системы) запускаются в порядке их написания (т.е. вторая задача запускается после окончания работы первой задачи), а данные передаются через промежуточный буфер.
Обычные операционные системы. ОС. К этому классу относятся такие широко распространенные системы, как VAX/VMS, системы семействаUnix, OS/2, Windows*. Здесь под ОС подразумеваются системы ``общего назначения'', т.е. рассчитанные на интерактивную работу одного или нескольких пользователей в режиме разделения времени. Как правило, в таких системах уделяется большое внимание защите самой системы, программного обеспечения и пользовательских данных от ошибочных и злонамеренных программ и пользователей. Обычно такие системы используют встроенные в архитектуру процессора средства защиты и виртуализации памяти.
Эволюция операционных систем
Последовательная обработка данных
Идеи создания вычислительных
машин давно витали в воздухе. В дневниках Леонардо да
Винчи можно найти эскизы вычислительной машины, на основе зубчатых элементов. В
1642г. Блез Паскаль создал реально работающее счетное устройство на основе
зубчатых колес, которое было в состоянии складывать и вычитать десятичные
числа.
1830-1846 гг. Чарльз Беббидж разрабатывает проект Аналитической машины - механической универсальной цифровой вычислительной машины с программным управлением (!). Машина состоит из пяти устройств - арифметического устройства (АУ), запоминающего устройства (ЗУ), устройства управления (УУ), ввода и вывода (все как в первых ЭВМ, появившихся 100 лет спустя). АУ строилось на основе зубчатых колес, на них же предлагалось реализовать ЗУ (на тысячу 50-разрядных чисел - итого 50 тыс. зубчатых колес). Для ввода программы и данных использовались перфокарты. Предполагаемая скорость вычислений: сложение и вычитание за 1 сек, умножение и деление - за 1 мин. Помимо арифметических операций, имелась команда условного перехода.
Первые работающие компьютеры появились в конце 40-х – начале 50-х гг. Фактически, ОС на них не было. Управление ЭВМ осуществлялось с тумблеров на пульте управления. Существовали некоторые устройства ввода данных (перфоленты, перфокарты), с которых можно было загрузить программу в память машины. В крайнем случае, задать значения ячеек памяти можно было непосредственно с тумблеров. О наличии каких либо ошибок сообщали соответствующие сигнальные лампы. С их помощью можно было проанализировать состояние памяти и регистров ЭВМ. Результаты работы программы можно было распечатать на принтере.
Распределение машинного времени происходило с помощью административных ресурсов: каждый пользователь записывался на определенное время. Если этого времени не хватало, то пользователь был вынужден прерывать работу.
В отведенное время пользователь должен был ввести в машину свою программу, откомпилировать ее (как правило, обычные программы были написаны на языке высокого уровня), скомпоновать программу с библиотечными функциями и запустить на счет. Возникновение каких либо ошибок приводило к необходимости начинать все заново.
Простые пакетные системы
Высокая стоимость процессорного времени привела к необходимости более эффективного его использования. В результате появилась концепция пакетной операционной системы. Первые пакетные ОС были разработаны в середине 50-х гг. в компании General Motors для машин IBM 701. В основе пакетных ОС лежит программа, называемая монитор. Основная часть монитора находится постоянно в оперативной памяти. Пользователь не имеет непосредственного доступа к машине. Вместо этого он общается с оператором. Оператор загружает последовательность перфокарт или перфоленту сразу нескольких заданий, после чего монитор загружает очередное задание, при необходимости производит с ним некоторые действия и отсылает на счет. После завершения счета управление возвращается монитору. Он сразу же закачивает следующее задание и система продолжает работу.
Многозадачные пакетные системы
Многозадачные пакетные системы являются логичным продолжением развития простых пакетных систем. При обработке одного задания могут возникать паузы, связанные, например, с операциями ввода/вывода. В простых пакетных системах процессор вынужден в таких ситуациях простаивать. Если же мы позволим нескольким задачам выполнять ``параллельно’’, последовательно выдавая каждой задаче свой квант времени, то мы получим возможность при приостановке одного процесса заставлять процессор обслуживать другой процесс. Это подразумевает наличие прерываний для осуществления операций ввода/вывода и наличие механизма управления памятью, т.к. все выполняемые программы обязаны одновременно находиться в физической памяти.
Системы, работающие в режиме разделения времени
Эти системы дают возможность
нескольким пользователям работать в системе параллельно в режиме on-line. Каждому процессу последовательно
выделяется свой квант времени для обслуживания процессором (величина кванта
обычно измеряется в миллисекундах). Отклик системы на действия пользователя
обычно наступает в течение нескольких секунд.
Считается, что первой операционной системой реального времени является ОС CTSS (Compatible Time-Sharing System). Она работала с оперативной памятью, состоящей из 32К 36-битных слов. Первые 5000 слов занимал монитор, а строго с адреса 5000 грузилась программа пользователя. С интервалом 0.2 секунды на место этой программы грузилась программа другого пользователя, а предыдущая спасалась на жестки диск. В качестве оптимизации этого процесса было предусмотрена выгрузка на диск не всей программы предыдущего пользователя, а только той части, которая затиралась новой программой, поэтому при восстановлении исходной программы с диска существовала в некоторых случаях возможность считывания не всей программы, а только ее затертой части.
Системы реального времени. Многопоточность. Потоки и процессы
Эти системы дают возможность нескольким пользователям работать в системе параллельно в режиме on-line, причем особые требования задаются для времени отклика системы на действия пользователей. Они должны происходить в режиме реального времени, т.е., практически, без задержек. В реальности, требование быстрого отклика системы заменяется требованием гарантированного отклика систему на любое событие в течение заданного интервала времени (действительно, если этот интервал зафиксирован, то, скорее всего, при развитии аппаратной части ЭВМ данный интервал будет уменьшаться, и в некоторой момент он, в любом случае, станет приемлемым).
Такому требованию заведомо не удовлетворяет ОС Windows 3.11. Windows 3.11 является кооперативной система, т.е. каждое приложение обязано само периодически проверять очередь сообщений. Только при каждой проверке система дает возможность другим приложениям передать управление процессором. Т.о., если приложение где-то зациклилось и не производит проверку очереди сообщений, то это подвешивает всю систему. Отметим, что это же свойство сохранилось для 16-битных приложений в Windows95, хотя для обычных 32-битных приложений здесь есть нормальные механизмы управления процессами.
К системам реального времени
применимо требование многопоточности.
С общим понятием `задачи’ обычно ассоциируются два понятия: поток (= нить = thread) и процесс. Обычно, под потоком понимают диспетчирезуемую единицу работы,
с которой связывается контекст процессора (например, регистр флагов), собственный
стек (который обычно задается регистром стека). Обычно потоки внутри одного
процесса имеют одно адресное пространство. Процесс является объединением
некоторого количества потоков вместе с набором ресурсов, связанных с потоками.
В отличие от потоков, различные процессы, вообще говоря, должны иметь различные
адресные пространства. Одна задача, вообще говоря, может состоять из нескольких
процессов, в каждом из которых может быть несколько нитей.
Вообще говоря, существуют и другие схемы соотношений потоков и процессов. Например, в ОС Clouds один поток может переходить от одного процесса к другому. Это очень удобно для реализации распределенных вычислений: поток ассоциируется с некоторой выполняемой последовательностью команд. При этом, можно переходить от одного адресного пространства к другому. Более того, эти адресные пространства могут относиться даже к разным ЭВМ.
Обычно к операционным системам реального времени предъявляют следующие требования:
1. ОС должна быть многонитевой и прерываемой.
2. Должно существовать понятие приоритета нити. Нить с высшим приоритетом должна иметь возможность прервать выполнение нити с низшим приоритетом.
3. ОС должна обеспечивать предсказуемые механизмы синхронизации задач (блокировка и посылка сигналов).
4. Должна существовать система наследования приоритетов. Это понятие связано с понятием инверсии приоритетов. Пусть запущено три процесса. Процесс с низшим из трех приоритетов может захватить некоторый ресурс А. Пусть сразу после этого запускается второй процесс с большим приоритетом, который вытесняет первый процесс. Далее запускается третий процесс с самым большим приоритетом и он тоже требует ресурс А. В результате получается блокировка: третий процесс не может продолжать работу, пока не первый процесс не освободит ресурс А, а первый процесс вынужден ждать завершения работы второго процесса. Т.о. на работу процесса с высшим приоритетом оказывает влияние процесс с низшим приоритетом. Эта ситуация называется инверсией приоритетов. Отметим, что эта ситуация весьма часто встречается в различных версиях Windows (в ранних версиях чаще, в более новых - реже).
Для выхода из этой ситуации ОС должна уметь повышать приоритет процесса с низшим приоритетом до приоритета процесса с высшим приоритетом, если второй процесс как-то обращается к первому процессу.
5. Поведение ОС должно быть известно. Например, должны быть известны времена выполнения всех системных вызовов, времена задержки от поступления прерывания до выполнения соответствующей процедуры и т.д.
Лекция 13
Базовые принципы функционирования вычислительных систем
Список литературы
Вильям Столлингс. Операционные системы. Москва. Издательский дом ``Вильямс’’.
2002.
С.В.Зубков. Ассемблер для DOS, Windows и UNIX.
Михаил Гук. Аппаратные средства IBM PC.
Системы реального времени. Многопоточность. Потоки и процессы
Эти системы дают возможность нескольким пользователям работать в системе параллельно в режиме on-line, причем особые требования задаются для времени отклика системы на действия пользователей. Они должны происходить в режиме реального времени, т.е., практически, без задержек. В реальности, требование быстрого отклика системы заменяется требованием гарантированного отклика систему на любое событие в течение заданного интервала времени (действительно, если этот интервал зафиксирован, то, скорее всего, при развитии аппаратной части ЭВМ данный интервал будет уменьшаться, и в некоторой момент он, в любом случае, станет приемлемым).
Такому требованию заведомо не удовлетворяет ОС Windows 3.11. Windows 3.11 является кооперативной система, т.е. каждое приложение обязано само периодически проверять очередь сообщений. Только при каждой проверке система дает возможность другим приложениям передать управление процессором. Т.о., если приложение где-то зациклилось и не производит проверку очереди сообщений, то это подвешивает всю систему. Отметим, что это же свойство сохранилось для 16-битных приложений в Windows95, хотя для обычных 32-битных приложений здесь есть нормальные механизмы управления процессами.
К системам реального времени
применимо требование многопоточности.
С общим понятием `задачи’ обычно ассоциируются два понятия: поток (= нить = thread) и процесс. Обычно, под потоком понимают диспетчирезуемую единицу работы,
с которой связывается контекст процессора (например, регистр флагов), собственный
стек (который обычно задается регистром стека). Обычно потоки внутри одного
процесса имеют одно адресное пространство. Процесс является объединением
некоторого количества потоков вместе с набором ресурсов, связанных с потоками.
В отличие от потоков, различные процессы, вообще говоря, должны иметь различные
адресные пространства. Одна задача, вообще говоря, может состоять из нескольких
процессов, в каждом из которых может быть несколько нитей.
Вообще говоря, существуют и другие схемы соотношений потоков и процессов. Например, в ОС Clouds один поток может переходить от одного процесса к другому. Это очень удобно для реализации распределенных вычислений: поток ассоциируется с некоторой выполняемой последовательностью команд. При этом, можно переходить от одного адресного пространства к другому. Более того, эти адресные пространства могут относиться даже к разным ЭВМ.
Обычно к операционным системам реального времени предъявляют следующие требования:
1. ОС должна быть многонитевой и прерываемой.
2. Должно существовать понятие приоритета нити. Нить с высшим приоритетом должна иметь возможность прервать выполнение нити с низшим приоритетом.
3. ОС должна обеспечивать предсказуемые механизмы синхронизации задач (блокировка и посылка сигналов).
4. Должна существовать система наследования приоритетов. Это понятие связано с понятием инверсии приоритетов. Пусть запущено три процесса. Процесс с низшим из трех приоритетов может захватить некоторый ресурс А. Пусть сразу после этого запускается второй процесс с большим приоритетом, который вытесняет первый процесс. Далее запускается третий процесс с самым большим приоритетом и он тоже требует ресурс А. В результате получается блокировка: третий процесс не может продолжать работу, пока не первый процесс не освободит ресурс А, а первый процесс вынужден ждать завершения работы второго процесса. Т.о. на работу процесса с высшим приоритетом оказывает влияние процесс с низшим приоритетом. Эта ситуация называется инверсией приоритетов. Отметим, что эта ситуация весьма часто встречается в различных версиях Windows (в ранних версиях чаще, в более новых - реже).
Для выхода из этой ситуации ОС должна уметь повышать приоритет процесса с низшим приоритетом до приоритета процесса с высшим приоритетом, если второй процесс как-то обращается к первому процессу.
5. Поведение ОС должно быть
известно. Например, должны быть известны времена выполнения всех системных
вызовов, времена задержки от поступления прерывания до выполнения
соответствующей процедуры и т.д.
Состояния процессов
В этом раздел мы не будем разделять понятия потока и процесса. Постараемся описать некоторые модели взаимодействия процессов, обеспечивающих их взаимосуществование. Будем предполагать, что система однопроцессорная, т.е. в один момент времени реально может выполняться только один процесс. Здесь имеется в виде, что в ОС существует понятие диспетчера. Под диспетчером подразумевается часть ОС, осуществляющая контроль за основным ресурсом ЭВМ – процессорным временем. Диспетчер с некоторой периодичностью передает право на использование процессора от одного процесса к другому.
Основной проблемой при сосуществовании процессов является необходимость дележа ими различных ресурсов. Основными ресурсами являются процессорное время и оперативная память. Кроме этого существуют устройства ввода/вывода, медленная скорость работы которых, собственно, и послужила одной из основных причин появления многозадачности.
Простейшая
модель из двух состояний
Пусть в системе одновременно находятся как минимум два процесса. Как мы договорились, в каждый момент времени может выполняться только один процесс. Тогда первое, что приходит в голову, это – ввести два основных состояния процессов: выполняется и не выполняется.

Новый процесс сразу после его появление в системе попадает в состояние не выполняется. Далее в некоторый момент диспетчер, если сочтет это возможным, может перевести данный процесс из состояния не выполняется в состояние выполняется. При этом, естественно, выполняющийся до этого процесс должен перейти в состояние не выполняется.
В некоторый момент, выполняющийся процесс может завершить свою работу и выйти из системы.
Возникает резонный вопрос: каким способом будет выбираться для выполнения очередной процесс, находящийся в состоянии не выполняется. Например, можно организовать очередь невыполняющихся процессов. Т.о. первым для выполнения из нее будет извлекаться процесс, который первым же в нее попал. Можно построить более сложную структуру, в которой будут организован список невыполняющихся процессов. При этом, очередной процесс для перевода в состояние выполняется будет выбираться по некоторому алгоритму.
Классическая
модель из пяти состояний
В модели, состоящей из двух состояний, легко увидеть следующий недостаток: на самом деле, процессы в состоянии не выполняется могут быть готовыми к дальнейшему выполнению, а могут не быть готовыми (когда некоторый им необходимый ресурс находится целиком в собственности другого процесса). Т.о. состояние не выполняется распадается на два принципиально различных состояния: готов к выполнению и блокированный:

Кроме этого, полезно выделить еще два важных состояния: новый и завершающийся.
Только что созданный процесс сразу же попадает в состояние новый. В этом состоянии проверяется возможность самого запуска процесса (в системе, например, может быть ограничение на количество запускаемых процессов), создается идентификатор процесса, заполняются все рабочие таблицы процесса. При этом, код программы еще не загружается в оперативную память. После загрузки всех необходимых данных и наличия всех необходимых ресурсов процесс может перейти в состояние готов.
В конце работы процесса также стоит выделить состояние завершающийся, когда, формально, процесс прекратил свою работу, но операционной системе еще необходимо выполнить некоторые операции по освобождению ресурсов, занятых процессом.
Готовый к выполнению процесс может быть переведен диспетчером в состояние выполняющийся, а после того, как данный процесс использовал свой квант процессорного времени, диспетчер может снова вернуть его в состояние готов, передав ресурс процессора другому процессу. В состояние готов из состояния выполняющийся процесс может перейти и по другим причинам. Например, может появиться второй процесс с большим приоритетом (или освободится ресурс, необходимый для выполнения второго процессу с большим приоритетом). В этом случае принято говорить, что второй процесс вытеснил первый.
Если окажется, что данный процесс претендует на ресурс, занятый другим процессом, то процесс переходит в состояние блокирован. При освобождении ресурса должно произойти какое-то событие (например, прерывание), которое укажет диспетчеру на то, что процесс следует перевести в состояние готов.
Для ускорения поиска процесса для перевода его из состояния блокирован в состояние готов можно распределить блокированные процессы по очередям, в каждой из которых располагаются процессы, ожидающие соответствующего события. Кроме того, имеет смысл выделить различные очереди для процессов с различными приоритетами (если в системе есть понятие приоритета).
Понятие свопинга.
Модель из шести или семи состояний
В реальной ОС существует довольно много процессов (сотни). При этом, многие процессы в данный момент не выполняют вообще никаких функций. Они могут, например, обслуживать некоторые устройства, которые в данный момент не используются и вообще не понятно когда будут использованы. В этом случае удобно полностью вытеснять такие процессы на диск (отметим, что понятие виртуальной памяти предполагает вытеснение неиспользуемой памяти на диск, но здесь речь идет о вытеснении всего процесса). Данный процесс переноса процессов на диск называется свопингом. При введении понятия свопинга придется ввести еще хотя бы одно состояние: приостановка. Процесс может перейти в приостановленное состояние из состояния блокирован, если в системе ощущается нехватка оперативной памяти:
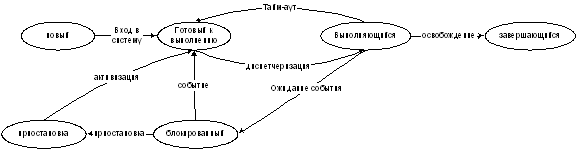
После того, как освободятся необходимые ресурсы, процесс может быть снова активирован и переведен в состояние готов к выполнению.
В реальности, при острой нехватке оперативной памяти процесс может переводиться в состояние приостановленный даже в том случае, когда он находился в состоянии готов. Т.е. в некоторых ОС следует подразделить состояния готовый/приостановленный и блокированный/приостановленный.
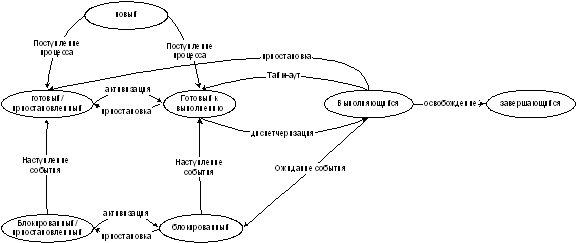
При этом, в состояние готовый/приостановленный процесс может попасть сразу из состояния выполняющийся, например, если его вытесняет процесс с большим приоритетом.
Понятие приостановки можно обобщить. Под этим состоянием можно понимать специальное состояние, когда процесс отсутствует в оперативной памяти и, самое главное, быть выведенным из этого состояние он может только при специальном запросе ОС или пользователя. Т.е. это выход из этого состояния не должен быть связанным с освобождением какого либо ресурса.
Основные принципы параллельных вычислений
Параллельные вычисления имеет смысл рассматривать в двух принципиально (по крайней мере, на первый взгляд) различных ситуациях: в случае однопроцессорной системы, в которой выполняется псевдо-параллельное выполнение нескольких процессов и в случае много-процессорной системы, когда присутствует реальное параллельное выполнение нескольких процессов.
Можно говорить о следующих основных проблемах, возникающих при параллельных вычислениях:
· Проблемы, возникающие при некорректном разделении доступа к глобальным объектам
· Проблемы, связанные со сложностью для ОС оптимального разделения ресурсов между процессами; при неоптимальном распределении ресурсов возможны явления, имеющие названия взаимоблокировки и голодание
· Сложность устойчивого повтора создавшихся ситуаций при отладке программ
Первую проблему можно проиллюстрировать следующим примером:
char *num2str(int n){static char s[100]; sprintf(s,”%d”,n); return s;}
Данная функция возвращает строку, в которой содержится текстовое представление параметра, передаваемого в функцию. Использование статической переменной удобно, т.к. не требует отведения/очистки памяти под строку. Однако, в многопоточной задаче использование подобной функции недопустимо, т.к. внутри одного процесса потоки имеют единое адресное пространство, и если два параллельных потока одновременно (или почти одновременно) вызовут эту функцию, то результат будет непредсказуемым.
Вторую проблему можно проиллюстрировать следующим простым примером: первый процесс сначала захватывает ресурс А, а потом требует захвата ресурса Б (не освобождая А). Параллельно второй процесс захватывает ресурс Б и далее требует захвата ресурса А. В результате, ни один из двух процессов не может продолжить свою работу. Данная ситуация называется взаимоблокировкой.
Третья проблема очевидна. При отладке многопроцессных приложений практически нереально воспроизвести создавшуюся ситуацию во второй раз, т.к. скорость работы каждого процесса зависит от очень большого количества разнообразных факторов. Более того, если мы пользуемся отладчиком, то он сам является процессом и, поэтому он также оказывает влияние на запущенные процессы. По сути, существует единственный способ отладки многопроцессных приложений: их надо сразу писать правильно J.
Вообще можно говорить о разных уровнях взаимодействия процессов, в зависимости от того, что процессы знают друг о друге. Если у процессов нет никакой информации друг о друге, то можно говорить о конкуренции процессов при попытке разделить общие ресурсы.
Если же какая-то информация друг о друге имеется, то говорят о сотрудничестве процессов при разделе ресурсов. При этом возможна ситуация, когда, на самом деле, процессы практически ничего друг о друге не знают, кроме того, что они используют один ресурс и изменения в этом ресурсе одного процесса могут использоваться другим процессом (сотрудничество при разделении ресурса). Или же процессы знают идентификатор друг друга и могут получать почти любую информацию друг о друге (сотрудничество при работе).
С каждым из описанных видов взаимодействия связаны соответствующие проблемы.
Конкуренция процессов в борьбе за ресурсы
Пусть есть два или более
процессов, которые ничего не знают друг о друге, но используют один неделимый
ресурс (см. пример функции, приведенной выше). В этом случае должен
существовать механизм взаимных исключений.
Этот механизм должен обеспечивать в определенных кусках кода каждого процесса
возможность использования данного ресурса не более чем одним процессом. Ресурс,
о котором идет речь, обычно называется критическим
ресурсом, а кусок кода процесса, в котором должно осуществляться
единовластие процесса над критическим ресурсом, принято называть критической секцией или критическим разделом (critical section).
Т.о., в коде программы должны быть обеспечены операторы начала критической секции (с указанием критического ресурса) и конца критической секции. При этом, мы сразу же получаем две новые проблемы: взаимные блокировки и голодание.
Сущность взаимной блокировки уже описана выше. Голодание наступает в результате более сложной ситуации. Пусть есть три процесса P1, P2, P3. Каждый из которых нуждается в каком либо неразделяемом ресурсе. Пусть процесс P1 получил доступ к ресурсу и успешно его использует. Параллельно ресурс потребовался процессам P2 и P3. Пусть процессы P1 и P2 имеют больший приоритет, чем процесс P3. Тогда после завершения использования ресурса процессом P1 начнет продолжит выполняться процесс P2. Пусть в процессе использования ресурса процессом P2 данный ресурс вновь потребовался процессу P1, а потом он снова потребовался процессу P2, и т.д. В результате ресурс будет переходить от процесса P1 к процессу P2 и наоборот, а процесс P3 так и не получит возможность продолжить работу, хотя, формально, взаимоблокировки не наступало. Данная ситуация носит название голодания.
Сотрудничество с использованием разделения
Пусть есть два или более
процессов, которые используют один ресурс по принципу сотрудничества по
использованию ресурса. При этом, результат воздействия на ресурс одного
процесса интересует другой процесс.
Простейший пример. У нас есть счетчик обращений к ресурсу: глобальная переменная n. Мы можем вызвать функцию увеличения счетчика:
void NInc(){n=n+1;}
а можем просто посмотреть значение переменной n. Отметим, что, вообще говоря, свободно использовать функцию в параллельных процессах нельзя, т.к. можно себе представить следующую последовательность действий по ее фактической реализации:
положить переменную n в регистр
увеличить переменную n на 1
положить значение регистра в переменную n
Теперь, если один процесс положит переменную в регистр и увеличит ее значение на 1, а другой процесс после этого прервет первый и сделает то же самое, то, в результате, в регистре будет лежать значение исходной переменной, увеличенное всего на 1, а не на 2, как хотелось бы. В результате при двух вызовах функции переменная n увеличится всего лишь на 1.
Т.о. в данной ситуации при вызове функции NInc следует помечать начало и конец критической секции. В отличие от предыдущей ситуации критическая секция предохраняет критический ресурс только от записи, но не от чтения. При выполнении функции NInc мы можем в любой момент использовать значение переменной n.
Однако, здесь появляется требование согласованности данных. Например, если у нас есть две переменных n1, n2, играющих в точности такую же роль, как и переменная n:
void NInc2(){n1=n1+1;n2=n2+1;}
то разумно потребовать, чтобы в каждый момент времени эти переменные совпадали бы. Однако, т.к. мы разрешили в любой момент времени использовать эти переменные, то при выполнении данной функции это условие может нарушаться. Проблема решается опять же с помощью критических секций.
Следующий пример еще более неприятен:
В одном процессе выполняется функция
void Add1(){n1++;
n2++;}
а в другом:
void Mult2(){n1*=2; n2*=2;}
Применение каждой функции не нарушает условие равенства переменных. Однако их одновременное применение может привести к следующей последовательности действий:
n1++;
n1*=2;
n2*=2;
n2++;
а в этом случае переменные перестанут быть равными.
В качестве решения проблемы можно предложить погружение каждого тела функции в критическую секцию для одного ресурса.
Сотрудничество с использованием связи
Пусть есть два или более процессов, которые знают идентификаторы друг друга и могут активно друг с другом общаться. Даже в этом случае возможны конфликты. Например, процесс P1 постоянно обменивается данными с процессами P2, P3. Голодание может возникнуть от того, что процесс P1 будет постоянно обмениваться данными с процессом P2, а процесс P3 будет сколь угодно долго ждать своей очереди.
Программная реализация. Алгоритм Деккера
Попробуем программно реализовать
механизм взаимоисключения для двух процессов. Мы хотим написать две функции:
void CriticalBegin();
void CriticalEnd();
которые вызываются, соответственно, в начале и в конце критической секции и обеспечивают выполнение критического кода в один момент не более, чем одним процессом. Приведем несколько попыток написания таких функций.
Попытка 1.
int Num=0;//указывает номер процесса,
занимающего критический ресурс
//Процесс 1:
void CriticalBegin()
{
while(Num==1);
}
void CriticalEnd();
{
Num=1;
}
//Процесс 2:
void CriticalBegin()
{
while(Num==0);
}
void CriticalEnd();
{
Num=0;
}
работает, но требует четкой чередуемости процессов при выполнении: сначала должен выполниться первый процесс, потом второй, потом снова первый, потом второй и т.д.
Попытка 2.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
//Процесс 1:
void CriticalBegin()
{
while(flag[1]==1);//пока ресурс занят вторым
процессом
flag[0]=1;//занять ресурс первым процессом
}
void CriticalEnd();
{
flag[0]=0;//освободить ресурс первым
процессом
}
//Процесс 2:
void CriticalBegin()
{
while(flag[0]==1);//пока ресурс занят первым процессом
flag[1]=1;//занять
ресурс вторым процессом
}
void CriticalEnd();
{
flag[1]=0;//освободить
ресурс вторым процессом
}
возможна ситуация, когда два процесса одновременно проверят условие в цикле while, убедятся, что ресурс свободен и далее начнут одновременно его использовать.
Попытка 3.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
//Процесс 1:
void CriticalBegin()
{
flag[0]=1;//занять
ресурс первым процессом
while(flag[1]==1);//пока ресурс занят вторым процессом
}
void CriticalEnd();
{
flag[0]=0;//освободить
ресурс первым процессом
}
//Процесс 2:
void CriticalBegin()
{
flag[1]=1;//занять
ресурс вторым процессом
while(flag[0]==1);//пока ресурс занят первым процессом
}
void CriticalEnd();
{
flag[1]=0;//освободить
ресурс вторым процессом
}
возможна ситуация, когда два процесса одновременно установят флаги и далее произойдет взаимная блокировка.
Попытка 4.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
//Процесс 1:
void CriticalBegin()
{
flag[0]=1;//занять
ресурс первым процессом
while(flag[1]==1)//пока ресурс занят вторым процессом
{//попали в коллизию
flag[0]=0;//освободим
на время ресурс
sleep(1);
flag[0]=1;//опять
займем ресурс
}
}
void CriticalEnd();
{
flag[0]=0;//освободить
ресурс первым процессом
}
//Процесс 2:
void CriticalBegin()
{
flag[1]=1;//занять
ресурс вторым процессом
while(flag[0]==1)//пока ресурс занят первым процессом
{//попали в коллизию
flag[1]=0;//освободим на время ресурс
sleep(1);
flag[1]=1;//опять займем ресурс
}
}
void CriticalEnd();
{
flag[1]=0;//освободить
ресурс вторым процессом
}
т.е., если мы попадаем в коллизию, то будем периодически уступать друг другу право использовать ресурс. Почти хорошо. Проблема возникнет, если два процесса будут выполняться строго синхронно. В этом случае также будет осуществляться взаимная блокировка.
Алгоритм Деккера.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
int Num=0;
//Процесс 1:
void CriticalBegin()
{
flag[0]=1;//занять
ресурс первым процессом
while(flag[1]==1)//пока ресурс занят вторым процессом
if(Num==1)//если надо уступить второму
процессу
{
flag[0]=0;//освободим
ресурс
while(Num==1);//подождем завершения второго процесса
flag[0]=1;//займем
ресурс
}
}
void CriticalEnd();
{
Num=1;
flag[0]=0;//освободить ресурс первым процессом
}
//Процесс 2:
void CriticalBegin()
{
flag[1]=1;//занять
ресурс вторым процессом
while(flag[0]==1)//пока ресурс занят первым процессом
if(Num==0)//если надо уступить первому процессу
{
flag[1]=0;//освободим
ресурс
while(Num==0);//подождем завершения первого процесса
flag[1]=1;//займем ресурс
}
}
void CriticalEnd();
{
Num=0;
flag[1]=0;//освободить
ресурс вторым процессом
}
Лекция 14
Базовые принципы функционирования вычислительных систем
Список литературы
Вильям Столлингс. Операционные системы. Москва. Издательский дом ``Вильямс’’.
2002.
С.В.Зубков. Ассемблер для DOS, Windows и UNIX.
Михаил Гук. Аппаратные средства IBM PC.
Взаимоисключения
Программная реализация. Алгоритм Деккера
Попробуем программно реализовать
механизм взаимоисключения для двух процессов. Мы хотим написать две функции:
void CriticalBegin();
void CriticalEnd();
которые вызываются, соответственно, в начале и в конце критической секции и обеспечивают выполнение критического кода в один момент не более, чем одним процессом. Приведем несколько попыток написания таких функций.
Попытка 1.
int Num=0;//указывает номер процесса,
занимающего критический ресурс
//Процесс 1:
void CriticalBegin()
{
while(Num==1);
}
void CriticalEnd();
{
Num=1;
}
//Процесс 2:
void CriticalBegin()
{
while(Num==0);
}
void CriticalEnd();
{
Num=0;
}
работает, но требует четкой чередуемости процессов при выполнении: сначала должен выполниться первый процесс, потом второй, потом снова первый, потом второй и т.д.
Попытка 2.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
//Процесс 1:
void CriticalBegin()
{
while(flag[1]==1);//пока ресурс занят вторым
процессом
flag[0]=1;//занять ресурс первым процессом
}
void CriticalEnd();
{
flag[0]=0;//освободить ресурс первым
процессом
}
//Процесс 2:
void CriticalBegin()
{
while(flag[0]==1);//пока ресурс занят первым процессом
flag[1]=1;//занять
ресурс вторым процессом
}
void CriticalEnd();
{
flag[1]=0;//освободить
ресурс вторым процессом
}
возможна ситуация, когда два процесса одновременно проверят условие в цикле while, убедятся, что ресурс свободен и далее начнут одновременно его использовать.
Попытка 3.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
//Процесс 1:
void CriticalBegin()
{
flag[0]=1;//занять
ресурс первым процессом
while(flag[1]==1);//пока ресурс занят вторым процессом
}
void CriticalEnd();
{
flag[0]=0;//освободить
ресурс первым процессом
}
//Процесс 2:
void CriticalBegin()
{
flag[1]=1;//занять
ресурс вторым процессом
while(flag[0]==1);//пока ресурс занят первым процессом
}
void CriticalEnd();
{
flag[1]=0;//освободить
ресурс вторым процессом
}
возможна ситуация, когда два процесса одновременно установят флаги и далее произойдет взаимная блокировка.
Попытка 4.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
//Процесс 1:
void CriticalBegin()
{
flag[0]=1;//занять
ресурс первым процессом
while(flag[1]==1)//пока ресурс занят вторым процессом
{//попали в коллизию
flag[0]=0;//освободим
на время ресурс
sleep(1);
flag[0]=1;//опять
займем ресурс
}
}
void CriticalEnd();
{
flag[0]=0;//освободить
ресурс первым процессом
}
//Процесс 2:
void CriticalBegin()
{
flag[1]=1;//занять
ресурс вторым процессом
while(flag[0]==1)//пока ресурс занят первым процессом
{//попали в коллизию
flag[1]=0;//освободим на время ресурс
sleep(1);
flag[1]=1;//опять займем ресурс
}
}
void CriticalEnd();
{
flag[1]=0;//освободить
ресурс вторым процессом
}
т.е., если мы попадаем в коллизию, то будем периодически уступать друг другу право использовать ресурс. Почти хорошо. Проблема возникнет, если два процесса будут выполняться строго синхронно. В этом случае также будет осуществляться взаимная блокировка.
Алгоритм Деккера.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
int Num=0;
//Процесс 1:
void CriticalBegin1()
{
flag[0]=1;//занять
ресурс первым процессом
while(flag[1]==1)//пока ресурс занят вторым процессом
if(Num==1)//если надо уступить второму
процессу
{
flag[0]=0;//освободим
ресурс
while(Num==1);//подождем завершения второго процесса
flag[0]=1;//займем ресурс
}
}
void CriticalEnd1();
{
Num=1;
flag[0]=0;//освободить ресурс первым процессом
}
//Процесс 2:
void CriticalBegin2()
{
flag[1]=1;//занять
ресурс вторым процессом
while(flag[0]==1)//пока ресурс занят первым процессом
if(Num==0)//если надо уступить первому процессу
{
flag[1]=0;//освободим
ресурс
while(Num==0);//подождем завершения первого процесса
flag[1]=1;//займем ресурс
}
}
void CriticalEnd2();
{
Num=0;
flag[1]=0;//освободить
ресурс вторым процессом
}
Программная реализация. Алгоритм Петерсона.
Алгоритм Петерсона представляет более простую реализацию взаимоисключений.
//указывает занятость ресурса, соответственно, первым и вторым процессами
int flag[2]={0,0};
int Num=0;
//Процесс 1:
void CriticalBegin1()
{
/*1.1*/ flag[0]=1;//занять
ресурс первым процессом
/*1.2*/ Num=1;//уступка права на критич.ресурс
второму процессу
/*1.3*/ while(flag[1]==1&&Num==1);//пока ресурс занят вторым процессом
}
void CriticalEnd1();
{
flag[0]=0;//освободить
ресурс первым процессом
}
//Процесс 2:
void CriticalBegin2()
{
/*2.1*/ flag[1]=1;//занять
ресурс вторым процессом
/*2.2*/ Num=0;//уступка права на критич.ресурс
первому процессу
/*2.3*/ while(flag[0]==1&&Num==0);//пока ресурс занят первым процессом
}
void CriticalEnd2();
{
flag[1]=0;//освободить
ресурс вторым процессом
}
Докажем, что оба процесса не могут одновременно попасть в критическую секцию. Допустим это так. Тогда рассмотрим три варианта.
1. При выполнении в последний раз сравнения в /*1.3*/ и /*2.3*/ сравнения производились одновременно (многопроцессорный случай). Тогда при сравнении выполнялось flag[0]==1 и flag[1]==1, но тогда либо Num==0 либо Num==1. Следовательно, одно из условий было истинным и выхода из цикла произойти не могло.
2. При выполнении в последний раз сравнения в /*1.3*/ и /*2.3*/ сравнение в /*1.3*/ выполнялось раньше. Тогда при этом выполнялось хотя бы одно из двух условий:
2.a. Num==0. Тогда до выхода из критической секции в первом процессе значение Num не могло смениться на 1, при этом, flag[0]==1. Следовательно во втором цикле выхода из цикла /*2.3*/ в течение этого времени произойти не могло.
2.б. flag[1]==0. Тогда операторы /*2.1*/ и /*2.2*/ должны были выполниться после сравнения в /*1.3*/. Т.о., при сравнении в /*2.3*/ должно выполняться Num==0 и flag[0]==1. Следовательно, во втором цикле выхода из цикла /*2.3*/ в течение этого времени произойти не могло.
3. При выполнении в последний раз сравнения в /*1.3*/ и /*2.3*/ сравнение в /*2.3*/ выполнялось раньше. Случай аналогичен случаю 2.
Итак, при всех рассмотренных случаях мы получил противоречие с одновременным нахождением двух процессов в критической секции, что доказывает невозможность данной ситуации.
¢
Осталось доказать, что для данного алгоритма невозможна взаимоблокировка, но это очевидно, т.к. условия циклов /*1.3*/ и /*2.3*/ не могут выполняться одновременно и измениться в самих циклах эти условия тоже не могут.
Аппаратная реализация. Отключение прерываний
Для случая однопроцессорной ЭВМ достаточно запретить прерывания при выполнении критической секции, что гарантирует, что в процессе ее выполнения перехода к другому процессу не произойдет.
Недостатки очевидны: подход неприменим для многопроцессорного случая. Кроме того, при зависании или зацикливании процесса в критической секции зависает вся система.
Аппаратная реализация. Использование машинных команд
Для реализации взаимоисключений можно использовать специальные машинные команды, которые должны поддерживаться соответствующей системой. Эти команды могут основываться на том, что изменение ячейки памяти может в один момент выполняться только одним процессом (т.е. контроллер памяти в любом случае должен поддерживать это свойство).
Например, пусть в системе есть атомарная команда изменения значения переменной вместе со сравнением ее с нулем:
int TestInc(int *v)
{
if(*v==0){*v=1; return 1;}
else return 0;
}
Т.о. мы предполагаем, что реализация этой функции имеет атомарный характер, т.е. только один процесс может заходить в функцию в один момент. Тогда взаимоисключения реализуются элементарно:
int num=0;//глобальная переменная
//…
{
while(TestInc(&num)==0);//ждем освобождения
ресурса
//критическая секция
num=0; //освобождаем ресурс
}
Очевидны достоинства и недостатки аппаратных реализаций взаимоисключений. Основные достоинства, это – простота и низкие накладные расходы. Недостатки – потенциальная возможность голодания и взаимоблокировок.
Семафоры
Одним из базовых понятий, используемых при реализации взаимных исключений, являются семафоры. Семафоры реализуются на уровне операционной системы, и их следует использовать просто как объекты, удовлетворяющие некоторым свойствам.
Семафор следует рассматривать как объект, содержащий целую переменную Count и очередь процессов ProcQueue. Над семафором можно совершать только три атомарных операции:
1. Инициализация переменной семафора Count неотрицательным числом.
2. Если значение Count меньше или равно 0, то блокировка текущего процесса и помещение его в очередь процессов ProcQueue Уменьшение переменной семафора Count на 1;.
3. Увеличение переменной семафора Count на 1; если значение Count становится меньше или равно 0, то из очереди процессов ProcQueue извлекается и разблокируется очередной процесс.
Вообще говоря, предполагается, что никаких других действий с семафорами осуществлять нельзя. На самом деле, в различных реализациях семафоров добавляются некоторые дополнительные действия, которые можно осуществить с семафорами. Например, в Linux реализованы следующие функции для работы с семафорами:
int sem_init(sem_t *sem, int pshared,
unsigned int Count);
int sem_wait(sem_t * sem);
int sem_trywait(sem_t * sem);
int sem_post(sem_t * sem);
int sem_getvalue(sem_t * sem, int *
sval);
int sem_destroy(sem_t * sem);
Функции описаны в файле semaphore.h.
Идентификатором семафора является объект типа sem_t.
Инициализируется семафор функцией
sem_init. В ней задаются:
· семафор, который следует инициализировать (указатель на sem_t),
· целая переменная pshared указывает на то, что семафор используется в различных процессах (pshared=1) или внутри одного процесса в различных нитях (pshared=0),
· целая переменная Count задает начальное значение семафора
Функция sem_wait проверяет значение семафора. Если значение семафора меньше или равно 0, то процесс (нить) блокируется. Далее функция уменьшает на 1 значение семафора.
Функция sem_post увеличивает на 1 значение семафора и, если необходимо, извлекает из очереди процессов ждущий заблокированный процесс и разблокирует его.
Дополнительные функции это:
int sem_trywait(sem_t * sem);
Если Count==0, то возвращает !0, иначе уменьшает Count на 1 и возвращает 0.
int sem_getvalue(sem_t
* sem, int * sval);
Возвращает значение семафора.
int sem_destroy(sem_t
* sem);
Очищает память из-под структуры данных, созданной sem_init.
Легко увидеть, что механизм взаимных исключений элементарно реализовать с помощью семафоров:
sem_t sem;
main()
{//инициализация
семафора:
sem_init(&sem,0,1);
//…
}
//функция
начала критической секции:
void CriticalBegin()
{
sem_wait(&sem);
}
//функция конца критической секции:
void CriticalEnd()
{
sem_post(&sem);
}
Задача о производителях и потребителях
Пусть есть несколько потребителей, которые производят штучный товар и кладут его на склад, и есть один потребитель, который берет товар со склада и потребляет. Следует разграничить права доступа производителей и потребителя к складу, так чтобы только один производитель или потребитель в один и тот же момент времени имел бы возможность пользоваться складом.
Задача является весьма распространенной. Например, несколько клиентов могут посылать текстовые сообщения серверу, а сервер должен выводить эти сообщения на экран по одному сообщению в строке (естественно, что в одной строке не должны смешиваться два сообщения от клиентов).
Пусть производитель производит
целые числа, а склад реализован в виде очереди на основе бесконечного массива
целых чисел m. Переменная in указывает
на номер ячейки в массиве m, куда производитель
должен класть очередное число. После помещения числа в массив in должна увеличиваться на 1. Переменная out указывает на номер
ячейки в массиве m, откуда потребитель должен
забирать очередное число. После извлечения числа из массива out должна увеличиваться на 1.
|
m0 |
m1 |
m2 |
m3 |
m4 |
… |
out in
Выделены элементы массива, лежащие на складе.
Попробуем написать программу,
реализующую описанную ситуацию. Чтобы не связываться с массивом=складом и
переменными in/out введем
целую переменную n=in-out, которая будет указывать на количество товара на складе.
Будем использовать следующие рабочие функции:
Produce(); //произвести единицу товара
Append(); //занести единицу произведенного товара
на склад
Take(); //взять единицу произведенного
товара со склада
Consume(); //использовать товар по назначению
Неудачная попытка.
Будем использовать два семафора: один - отвечающий за блокировку при обращении к складу (prod), другой - позволяющий потребителю спать, пока на складе ничего нет (cons).
Инициализация семафоров:
sem_t prod,cons; int
n=0;
main()
{
sem_init(&prod,0,1);//изначально склад
готов к обслуживанию товара
sem_init(&cons,0,0);//изначально
потребителю нечего потреблять
//…
}
Итак, на первый взгляд, функция, отвечающая за производство в каждом процессе-производителе может иметь следующий вид:
void P0()
{
while(1)//вечно производить
{
Produce(); //произвести единицу товара
sem_wait(&prod);//начало критической
секции
Append(); //занести единицу произведенного товара на
склад
n++;
if(n==1)//при
поступлении первого товара разблокировать потребителя
sem_post(&cons);
sem_post(&prod); //конец критической секции
}
}
функция, отвечающая за потребление в процессе-потребителе может иметь следующий вид:
void P1()
{
sem_wait(&cons);//ждать первого товара
на складе
while(1)//вечно
потреблять
{
sem_wait(&prod);//начало критической
секции
Take(); //изъять
единицу произведенного товара со склада
n--;
sem_post(&prod); //конец критической
секции
Consume();
//употребить единицу товара
if(n==0)//при отсутствии товара на складе заблокировать потребление
sem_wait(&cons);
}
}
Отметим, что, совершенно логично, функции производства/потребления вынесены за рамки критических секций, т.к. критическому ресурсу они не обращаются, а время их выполнения, наверняка, весьма существенно.
Оказывается, что приведенный алгоритм неверен. Вкратце, это можно проиллюстрировать следующим образом. Пусть выполнилась следующая последовательность действий:
· произвели товар ( Þ n==1 ; значение cons == 1 )
· изъяли товар со склада и потребляем его в функции Consume(); ( Þ n==0 )
· снова произвели товар ( Þ n==1 ; значение cons == 2)
· проверили в P1 условие if(n==0); оно оказалось ложью, поэтому значение cons не изменилось
· потребили товар ( Þ n==0 ; значение cons == 2)
· проверили в P1 условие if(n==0); оно оказалось истиной, поэтому значение cons уменьшилось ( Þ n==0 ; значение cons == 1), но блокировка для cons не наступила, т.к. cons > 0
· пытаемся снова потребить товар, но склад пуст. Неприятности.
Правильное решение.
Проблема в предыдущем примере заключалась в том, что у нас нарушился баланс между инкрементациями и декрементациями семафора. Мы инкрементировали семафор каждый раз, когда выполнялось n==1 и должны были декрементировать его каждый раз, когда выполнялось n==0, но последнее требование мы не выполнили.
Чтобы не пропустить случай n==0 , мы можем ввести временную переменную n1 и присвоить ей значение n внутри критической секции. Теперь нулевое значение n не пропадет, т.к. сравнение if(n==0) мы заменим на сравнение if(n1==0).
Итого, правильный вариант функции, отвечающей за потребление:
void P1()
{int n1;
sem_wait(&cons);//ждать
первого товара на складе
while(1)//вечно
потреблять
{
sem_wait(&prod);//начало критической
секции
Take(); //изъять
единицу произведенного товара со склада
n--; n1=n;
sem_post(&prod); //конец критической
секции
Consume();
//употребить единицу товара
if(n1==0)//при отсутствии товара на складе заблокировать потребление
sem_wait(&cons);
}
}
Более короткое решение.
На самом
деле, переменная n является лишней, т.к. семафор cons сам является счетчиком. Поэтому
функции могут иметь следующий вид:
void P0()
{
while(1)//вечно
производить
{
Produce(); //произвести единицу товара
sem_wait(&prod);//начало критической
секции
Append(); //занести единицу произведенного товара на
склад
sem_post(&prod); //конец критической секции
sem_post(&cons);//добавить 1 к семафору
потребителя
}
}
void P1()
{
while(1)//вечно
потреблять
{
sem_wait(&cons);//ждать товара на
складе
sem_wait(&prod);//начало критической
секции
Take(); //изъять
единицу произведенного товара со склада
sem_post(&prod); //конец критической секции
Consume();
//употребить единицу товара
}
}
Отметим, перестановка sem_post(&prod); и sem_post(&cons); в P0 ничего не изменит, т.к.для изъятия товара надо разблокировать оба семафора. А вот перестановка sem_wait(&cons); и sem_wait(&prod); в P1 приведет к неприятным последствиям. В этом случае, если потребитель войдет в критическую секцию при пустом складе, то производитель уже никогда не сможет воспользоваться складом. Возникнет взаимоблокировка.