Сбалансированные и идеально сбалансированные бинарные деревья поиска

Бинарное дерево называется сбалансированным, если для любой его вершины v высоты левого и правого поддерева, выходящих из v (т.е. поддеревьев с корнями v->left и v->right), отличаются не более чем на 1.

Бинарное дерево называется идеально сбалансированным, если длины всех ветвей, начинающихся в корне дерева и заканчивающихся в узле с хотя бы одним из нулевых указателей v->left и v->right, отличаются не более чем на 1.

В литературе встречается другое (неравносильное) определение идеально сбалансированных деревьев. Будем называть идеально сбалансированными’ деревьями такие деревья, для которых для каждой вершины количество элементов в левом и правом поддереве отличается не более, чем на единицу.

Следующее условие равносильно условию идеально сбалансированности дерева: длины любых двух ветвей, начинающихся в одной вершине дерева, отличаются не более чем на 1. Доказательство тривиально. Из данного условия сразу же вытекает

Теорема. Идеально сбалансированное дерево является сбалансированным.

Иными словами, можно сказать, что для идеально сбалансированного дерева полностью заполнены элементами все слои дерева, кроме, быть может, последнего. Т.о. для идеально сбалансированного дерева высоты h количество элементов лежит в пределах 2^h-1£N<2^h. из чего сразу же вытекает следующая элементарная

Теорема. Для идеально сбалансированного дерева, состоящего из N вершин, высота дерева h лежит в пределах

log₂ N < h £ 1+ log₂ N.

Оказывается, верна следующая

Теорема. Идеально сбалансированное’ дерево является идеально сбалансированным.

Доказательство. Докажем данную теорему по индукции. Для деревьев высоты не более 1 теорема верна. Пусть для деревьев высоты h теорема верна, докажем ее для деревьев высоты h +1.

По определению идеально сбалансированных’ деревьев, каждое поддерево такого дерева – идеально сбалансировано’, а по условию индукции левое и правое поддеревья корня дерева высоты h+1 – идеально сбалансированы. В идеально сбалансированных деревьях высоты l для количества элементов дерева N выполнено соотношение 2^l-1£N<2^l, из чего сразу вытекает: если у двух идеально сбалансированных деревьев количество элементов в них отличается не более, чем на единицу, то либо их высоты равны, либо (если количество элементов в них, соответственно, равно 2^l-1 и 2^l) в меньшем дереве последний слой полностью заполнен. В обоих случаях длины всех ветвей обоих деревьев, начинающихся в корне, заканчивающихся в вершинах, не имеющих хотя бы одного потомка, отличаются не более, чем на единицу. Отсюда сразу вытекает, что и для дерева, полученного с помощью объединения двух таких деревьев с помощью общего корневого элемента, длины всех ветвей, начинающихся в корне, заканчивающихся в вершинах, не имеющих хотя бы одного потомка, отличаются не более, чем на единицу.

¢

Для сбалансированного дерева верна оценка высоты дерева через количество вершин в нем, аналогичная по порядку оценке для идеально сбалансированных деревьев.

Теорема. Для сбалансированного дерева, состоящего из N вершин, высота дерева h имеет оценку:

h =Q( log₂ N ).

Доказательство. Пусть t_n – минимальное количество элементов в сбалансированном дереве высоты n. Тогда верна рекурсивная формула

t_n=t_n-1+t_n-2+1

т.е. для сбалансированного дерева высоты n с минимальным количеством вершин одно из поддеревьев, дочерних корневому элементу, должно быть сбалансированным деревом высоты n-1 с минимальным количеством вершин, а другое - сбалансированным деревом высоты n-2 с минимальным количеством вершин.

Уравнение t_n-t_n-1-t_n-2=1 имеет общее решение вида

t_n=с₁l₁ⁿ + с₁l₂ⁿ –1

где l_i являются решениями уравнения l²-l-1=0. Из этого следует, что

t_n= ( (1+sqrt(5))/2 )ⁿ (1+o(1))

после логарифмирования последнего равенства мы сразу получаем требуемое соотношение:

log₂ C₁ + log₂ t_n ≥ n log₂ ( (sqrt(5)+1)/2 )

n ≤ (log₂ t_n + log₂ C₁)/ log₂ ( (sqrt(5)+1)/2 )

для некоторого C₁>0. Или, в исходных обозначениях,:

h ≤ log₂ N / log₂ ( (sqrt(5)+1)/2 )+ log₂ C₂ ≤ 1.45 log₂ N+ C

¢

Операции с идеально сбалансированным деревом

Выше мы описали ряд алгоритмов выполнения базовых операций для деревьев поиска. К сожалению, не существует быстрых алгоритмов, для выполнения этих операций для идеально сбаланированных деревьев. Однако, определение идеально сбаланированного’ дерева, фактически, дает нам алгоритм его построения, что сразу же дает нам возможность строить и идеально сбаланированное дерево по тому же набору элементов. Для построения идеально сбаланированного’ дерева по набору из N элементов упорядочим этот набор. После этого алгоритм построения дерева сводится к разбиению полученной последовательности {a_i}_i=1,…,N на последовательности {a_i}_{i=1,…,[N/2]} и {a_i}_{i=[N/2]+2,…,N}. Эти последовательности либо имеют равную длину (для нечетных N), либо их длина отличается не более, чем на единицу (для четных N). В корень создаваемого дерева помещаем элемент a_[N/2]+1 , а левое и правое поддеревья строим таким же алгоритмом, соответственно, для последовательностей {a_i}_{i=1,…,[N/2]} и {a_i}_{i=[N/2]+2,…,N}.

Итак, приведенный алгоритм доказывает следующую теорему:

Теорема. Идеально сбалансированное’ (а значит и идеально сбалансированное) дерево поиска, состоящее из N вершин, можно построить за время, равное O(N log₂ N).

Таким образом, идеально сбалансированные деревья поиска удобны в тех случаях, когда перестройку дерева требуется производить, относительно редко, но требуется часто искать элементы в дереве. Приведенная оценка на высоту дерева гарантирует, что данная структура данных является наилучшей, с точки зрения времени поиска элементов в множестве (отметим, что здесь мы рассматриваем толко алгоритмы поиска, основанные на сравнениях). Все остальные операции (добавления элементов, удаления элементов и т.д.) в идеально сбалансированном дереве производятся с помощью полной перестройки дерева, т.е. они производятся медленно.

Отметим, что наша задача выродилась. Идеально сбалансированные деревья полезны только для поиска элементов в этих деревьях, но тогда дерево вообще не нужно строить! Достаточно ограничиться упорядоченным массивом исходных элементов, а поиск производить с помощью бинарного поиска. В этом случае, согласно построению идеально сбалансированного дерева’, поиск по дереву будет в точности совпадать с поиском по массиву, что делает само дерево ненужным.

Операции со сбалансированным деревом

Оказывается, что для сбалансированных деревьев все описанные выше операции можно модифицировать так, что они будут сохранять сбалансированность дерева, при этом, время их выполнения не будет превышать O(log₂ N) операций. Везде далее, говоря о сбалансированных деревьях, будем подразумевать, что мы имеем дело с сбалансированными деревьями поиска.

Правым и левым поддеревьями некоторой вершины дерева v называются поддеревья с корнями v->left и v->right, соответственно.

Балансом вершины дерева будем называть разность высот левого и правого поддеревьев этой вершины.

Поиск элемента в дереве

Не отличается от случая стандартных деревьев поиска.

Добавление элемента в дерево

Рассмотрим вершину дерева a, в которой нарушается баланс после добавления элемента. Все нижесказанное будет верным, если это не оговорено особо, и для случая какого-либо изменения одного из поддеревьев вершины a, приводящего к удлинению/укорачиванию соответствующего дерева на 1.

Будем предполагать, что для всех вершин, лежащих ниже a, баланс по модулю не превосходит 1.

Пусть, для определенности, элемент добавляется в левое поддерево вершины a. Справа и сверху от вершины будем писать баланс вершины после добавления новой вершины, а рядом, в круглых скобках, - баланс до добавления. Высоту соответствующего данной вершине поддерева будем писать справа снизу от вершины.

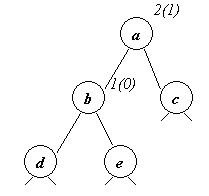
То, что дерево после добавления вершины разбалансировалось, означает, что до добавления вершины [a]=1, а после добавления [a]=2 (будем обозначать баланс вершины с помощью квадратных скобок: баланс вершины a = [a]). Возможны три случая баланса вершины b после изменения дерева: 1, 0, -1. Рассмотрим их

1.После добавления вершины [b]=1 или 0 (или изменения поддерева с корнем b) ([b]=1 соответствует удлинению левого поддерева b)

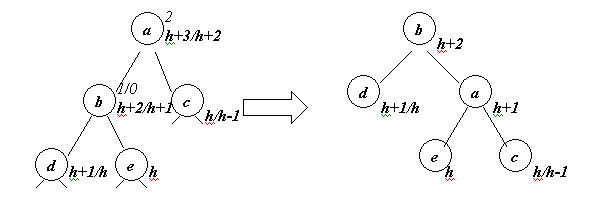
На рисунке варианты [b]=1 или 0 печатаются через слеш (косую черту).

Приведенную здесь перестановку вершин (с соответствующими поддеревьями) будем называть правым поворотом (в соответствии с перемещением вершин d-b-a).

Будем обозначать высоты дерева с корнем в вершине x h_x , а баланс этой вершины [x].

Пусть h_e=h, тогда для случая [b]=1

h_d=h+1 (т.к. [b]=1)

h_b=h+2

h_a=h+3

h_c=h (т.к. [a]=2)

Из чего сразу следует, что после правого поворота

[a]=[b]=0

[c], [d], [e] не изменились

Т.о. данное дерево сбалансировалось. При этом, если изменение дерева произошло в результате добавления вершины, его высота не изменилась. Действительно, перед добавлением вершины h_d=h из чего следует, что перед добавлением вершины h_a=h+2. После добавления высота не изменилась. Т.о. в случае [b]=1 процесс балансировки дерева завершен.

Для случая [b]=0 нарисованное дерево тоже остается сбалансированным:

h_d=h (т.к. [b]=0)

h_b=h+1

h_a=h+2

h_c=h-1 (т.к. [a]=2)

Из чего сразу следует, что после правого поворота

[a]=1, [b]=-1

[c], [d], [e] не изменились.

Однако высота всего нарисованного дерева изменяется (была до добавления h_a=h+1, стала h_a=h+2).

Итак, если перед изменением дерева h_b=1, то процесс балансировки завершен. Иначе, может разбалансироваться родитель вершины a, и для нее нужно выполнить тот же алгоритм.

2.После добавления вершины [b]=-1 (или изменения поддерева с корнем b) (удлинение правого поддерева b)

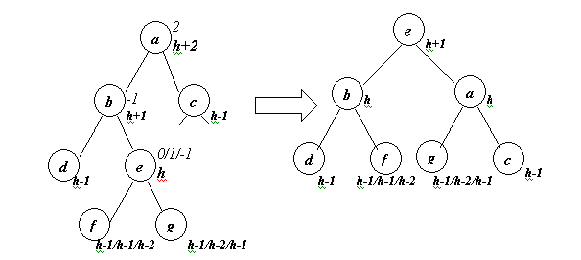
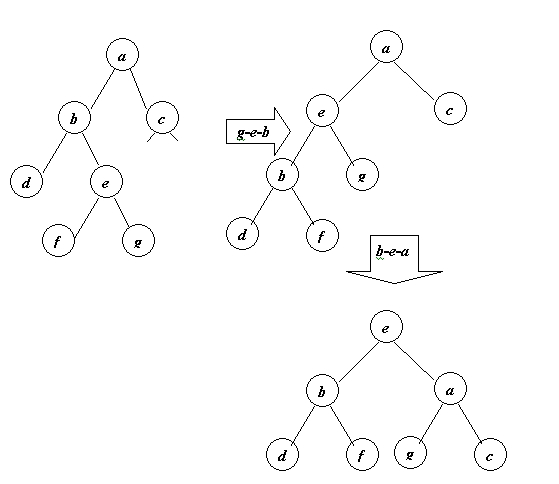
Описанная перестановка может быть проведена за два вращения: левого g-e-b и правого b-e-a:

Возможны три варианта баланса c: [c]=0/1/-1. Пусть h_e=h, тогда, в соответствии с возможными вариантами [c] имеем:

h_f=h-1/h-1/h-2

h_g=h-1/h-2/h-1

h_d=h-1

h_b=h+1

h_a=h+2

h_c=h-1

Из чего сразу следует, что после правого поворота

[b]=0/0/1

[a]=0/-1/0

[e]=0

[d], [f] , [g] , [c] не изменились.

Т.о. данное нарисованное дерево сбалансировалось. При этом, если изменение дерева произошло в результате добавления вершины, его высота не изменилась. Действительно, перед добавлением вершины h_e=h-1 из чего следует, что перед добавлением вершины h_a=h+1. После добавления высота не изменилась. Т.о. в случае добавления вершины при [b]=-1 процесс балансировки дерева завершен.

Т.о. процедура вставки вершины в сбалансированное дерево поиска сводится к нахождению вершины v, после которой следует вставить новую вершину и проверке условия сбалансированности всех вершин на ветке, завершающейся в v. Причем, проверку надо вести от вершины v к корню и если встретится разбалансированная вершина, то с помощью одного или двух вращений все дерево можно привести к сбалансированному.

Итак, мы доказали следующую теорему

Теорема. В сбалансированное дерево поиска, состоящее из N вершин, можно добавить одну вершину за время O(log₂ N). При этом, для балансировки дерева потребуется не более двух поворотов.

Отметим, что хотя балансировок требуется не более двух, весь процесс балансировки, все же, требует времени O(log₂ N), т.к. требуется еще найти – в какой вершине следует производить балансировку.

Удаление элемента из дерева

Удаление вершины из дерева поиска описано в параграфе Бинарные деревья поиска. Нам остается только сбалансировать, возможно, разбалансированное дерево.

Т.о. процедура удаления вершины v из сбалансированного дерева поиска сводится к следующему

· нахождению вершины v, которую следует удалить,

· ее удаления из дерева поиска (с помещением на ее место некторой вершины v'),

· для каждой вершины ветви дерева от v' до корня следует проверять условие балансировки – если оно нарушилось, то операциями вращения следует произвести балансировку соответствующего поддерева.

Итак, в силу построения алгоритма удаления вершины из сбалансированного дерева, верна

Теорема. Из сбалансированного дерево поиска, состоящего из N вершин, можно удалить одну вершину за время O(log₂ N).

Поиск минимального и максимального элемента в дереве

Не отличается от случая стандартных деревьев поиска.

Поиск следующего/предыдущего элемента в дереве

Не отличается от случая стандартных деревьев поиска.

Слияние двух деревьев

Для двух сбалансированных деревьев поиска T₁ и T₂ таких, что все элементы в T₁ меньше или равны всех элементов в T₂ : слияние деревьев в одно дерево поиска T.

Выбираем из дерева T₂ наименьший элемент v (самый левый) и удаляем его из дерева T₂ . Элемент v называется стыковочным. Для него верно: T₁£ v£ T₂ .

Возможна ситуация, когда стыковочный элемент присутствует уже в постановке задачи.

Будем, для определенности, предполагать, что высота дерева T₁ больше или равна высоте дерева T₂.

Рассмотрим правую ветвь дерева T₁ : {v₁,…,v_K}. В силу сбалансированности дерева имеем: h(v_i) - h(v_i+1) £ 2, тогда на этой ветви найдется вершина v_l, такая что

h(v_l) = h(T₂) или h(v_l) = h(T₂)+1

Сольем дерево с корнем в v_l и T₂ с помощью стыковочной вершины v и подставим новое дерево на место старой вершины v_l.

Вершина v_l и все дерево, с нее начинающееся, окажутся сбалансированными. Высота же дерева, начинающегося с v_l, увеличится на 1, т.к. h(T₂) £h(v_l) .

Итак, в результате изменений дерева у одной вершины w длина соответствующего поддерева увеличилась на 1. Далее нам следует запустить стандартную процедуру балансировки дерева. Мы должны пройти ветвь, заканчивающуюся на w, от w до корня и в каждой вершине проверить баланс. Если он будет по модулю больше 1, то баланс в данной вершине следует скорректировать одним или двумя вращениями.

Если, при этом, длина данного поддерева восстановится до значения, которому она была равна до слияния деревьев, то далее процесс проверки сбалансированности производить не надо (т.к. дерево T₁ до слияния было сбалансированным). Иначе, процесс проверки следует продолжить.

Отметим, что, в отличии от добавления к дереву одной вершины, в данном случае после уравновешения одной вершины процесс может не завершиться, т.к. возможен следующий вариант

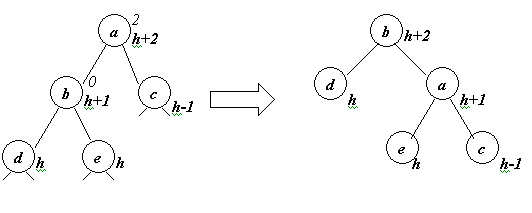
Этот вариант не мог реализоваться при добавлении одной вершины к дереву. В этом случае до слияния деревьев высота дерева с корнем a была равна h+1, а после слияния она стала равной h+2.

Итак, в силу построения алгоритма слияния двух сбалансированных деревьев, верна

Теорема. Для двух сбалансированных деревьев поиска T₁ и T₂ , состоящих из N₁ и N₂ вершин, имеющих высоты h₁ и h₂, и элемента v, таких, что все элементы в T₁ меньше или равны v и v меньше или равно всех элементов в T_{2 :} слияние деревьев с помощью стыковочного элемента v в одно сбалансированное дерево поиска T можно произвести за время T=O(log₂ (N₁+N₂) ) или за время T=O(|h₁-h₂|). Указанные деревья T₁ и T₂ можно слить за время T=O(log₂ (N₁+N₂) ).

Отметим здесь, что для слияния двух сбалансированных деревьев требуется сначала извлечения стыковочный элемент из дерева с большей высотой, поэтому эта операция требует большего времени, чем слияние деревьев с готовым стыковочным элементом.

Разбиение дерева по разбивающему элементу

Для данной вершины дерева v разбиение сбалансированного дерева поиска T на два сбалансированных дерева поиска T₁ и T₂ таких, что все элементы в T₁ меньше или равны v, и все элементы в T₂ больше или равны v.

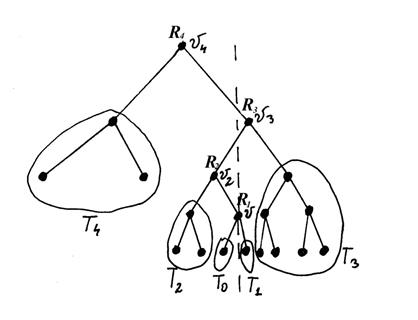
Алгоритм, практически полностью, совпадает с алгоритмом разбиения обычного дерева поиска. Только, теперь, нам следует пользоваться алгоритмом слияния деревьев для сбалансированных деревьев поиска.

Пусть высота дерева T₀ равна s₀. Пусть с деревом T₀ будут последовательно сливаться деревья T с индексами i₁,…,i_K (i_K£h), в результате чего будут получаться деревья S₁, S₂,…, S_K . Будем считать S₀= T₀. Т.е. S_j-1+ T_ij ® S_j .

Высота дерева S_j равна либо MAX(h(S_j-1),h(T_ij )), либо MAX(h(S_j-1),h(T_ij ))+1.

Пусть R_i – деревья с корнями в вершинах v_i. Высота дерева R_i равна либо h(T_i)+1 либо h(T_i)+2. h(R_i) строго возрастают.

Покажем по индукции , что высота дерева S_j равна либо h(R_ij), либо h(R_ij)-1, либо h(R_ij)-2. Пусть данное свойство выполнено для l<j, тогда

h(S_j )=MAX(h(S_j-1),h(T_ij )) | MAX(h(S_j-1),h(T_ij ))+1 следовательно

h(S_j )= MAX(h(S_j-1),h(R_ij) -1) | MAX(h(S_j-1),h(R_ij) -2) |

MAX(h(S_j-1),h(R_ij) -1)+1 | MAX(h(S_j-1),h(R_ij) -2)+1 следовательно по индукции

h(S_j )= (h(R_ij) -1) | ((h(R_ij) -1) | h(R_ij) -2) |

h(R_ij) | (h(R_ij) | h(R_ij) -1) следовательно

h(S_j )= h(R_ij) | (h(R_ij) -1) | (h(R_ij) -2)

Здесь под вертикальной чертой подразумевается разделение возможных вариантов.

Время работы всего алгоритма

T=O(|h(T₀)- h(T_i1 )|+1 +| h(S₁)- h(T_i2 )|+1 +…+| h(S_K-1) - h(T_iK )|+1)=

=O(|h(T₀)- h(T_{i1 )}| +| h(S₁)- h(T_i2 )| +…+| h(S_K-1) - h(T_iK )|)+O(h)=

=O(|h(T₀ )- h(R_i1 )|+4 +| h(R_i1 )- h(R_i2 )|+4 +…+| h(R_i(K-1) ) - h(R_iK )|+4)+O(h)=

(в силу возрастания h(R_i) )

=O(|h(T₀ )- h(R_i1 )|+| h(R_i1 )- h(R_i2 )|+…+| h(R_i(K-1) ) - h(R_iK )|)+O(h)= O(h)

Т.о. T= O(h)=O(log₂ N), где N – количество вершин в суммарном дереве.

Итак, верна следующая

Теорема. Для данной вершины v сбалансированного дерева поиска T разбиение на два сбалансированных дерева поиска T₁ и T₂ таких, что все элементы в T₁ меньше или равны v, и все элементы в T₂ больше или равны v. может быть произведено указанным алгоритмом за время = O(log₂ N), где N – суммарное количество вершин в деревьях T₁ и T₂.