Слияние двух деревьев

Для двух сбалансированных деревьев поиска T₁ и T₂ таких, что все элементы в T₁ меньше или равны всех элементов в T₂ : слияние деревьев в одно дерево поиска T.

Выбираем из дерева T₂ наименьший элемент v (самый левый) и удаляем его из дерева T₂ . Элемент v называется стыковочным. Для него верно: T₁£ v£ T₂ .

Возможна ситуация, когда стыковочный элемент присутствует уже в постановке задачи.

Будем, для определенности, предполагать, что высота дерева T₁ больше или равна высоте дерева T₂.

Рассмотрим правую ветвь дерева T₁ : {v₁,…,v_K}. В силу сбалансированности дерева имеем: h(v_i) - h(v_i+1) £ 2, тогда на этой ветви найдется вершина v_l, такая что

h(v_l) = h(T₂) или h(v_l) = h(T₂)+1

Сольем дерево с корнем в v_l и T₂ с помощью стыковочной вершины v и подставим новое дерево на место старой вершины v_l.

Вершина v_l и все дерево, с нее начинающееся, окажутся сбалансированными. Высота же дерева, начинающегося с v_l, увеличится на 1, т.к. h(T₂) £h(v_l) .

Итак, в результате изменений дерева у одной вершины w длина соответствующего поддерева увеличилась на 1. Далее нам следует запустить стандартную процедуру балансировки дерева. Мы должны пройти ветвь, заканчивающуюся на w, от w до корня и в каждой вершине проверить баланс. Если он будет по модулю больше 1, то баланс в данной вершине следует скорректировать одним или двумя вращениями.

Если, при этом, длина данного поддерева восстановится до значения, которому она была равна до слияния деревьев, то далее процесс проверки сбалансированности производить не надо (т.к. дерево T₁ до слияния было сбалансированным). Иначе, процесс проверки следует продолжить.

Отметим, что, в отличии от добавления к дереву одной вершины, в данном случае после уравновешения одной вершины процесс может не завершиться, т.к. возможен следующий вариант

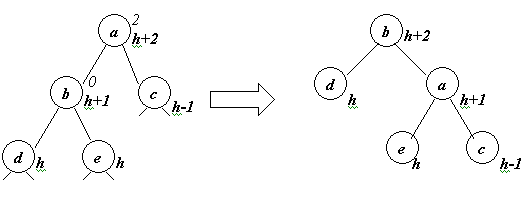
Этот вариант не мог реализоваться при добавлении одной вершины к дереву. В этом случае до слияния деревьев высота дерева с корнем a была равна h+1, а после слияния она стала равной h+2.

Итак, в силу построения алгоритма слияния двух сбалансированных деревьев, верна

Теорема. Для двух сбалансированных деревьев поиска T₁ и T₂ , состоящих из N₁ и N₂ вершин, имеющих высоты h₁ и h₂, и элемента v, таких, что все элементы в T₁ меньше или равны v и v меньше или равно всех элементов в T_{2 :} слияние деревьев с помощью стыковочного элемента v в одно сбалансированное дерево поиска T можно произвести за время T=O(log₂ (N₁+N₂) ) или за время T=O(|h₁-h₂|). Указанные деревья T₁ и T₂ можно слить за время T=O(log₂ (N₁+N₂) ).

Отметим здесь, что для слияния двух сбалансированных деревьев требуется сначала извлечения стыковочный элемент из дерева с большей высотой, поэтому эта операция требует большего времени, чем слияние деревьев с готовым стыковочным элементом.

Разбиение дерева по разбивающему элементу

Для данной вершины дерева v разбиение сбалансированного дерева поиска T на два сбалансированных дерева поиска T₁ и T₂ таких, что все элементы в T₁ меньше или равны v, и все элементы в T₂ больше или равны v.

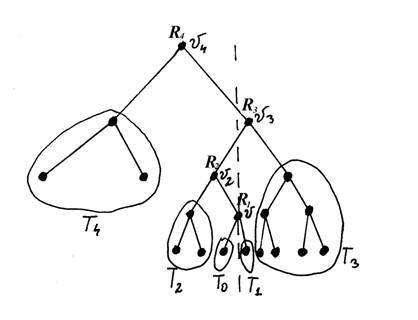
Алгоритм, практически полностью, совпадает с алгоритмом разбиения обычного дерева поиска. Только, теперь, нам следует пользоваться алгоритмом слияния деревьев для сбалансированных деревьев поиска.

Пусть высота дерева T₀ равна s₀. Пусть с деревом T₀ будут последовательно сливаться деревья T с индексами i₁,…,i_K (i_K£h), в результате чего будут получаться деревья S₁, S₂,…, S_K . Будем считать S₀= T₀. Т.е. S_j-1+ T_ij ® S_j .

Высота дерева S_j равна либо MAX(h(S_j-1),h(T_ij )), либо MAX(h(S_j-1),h(T_ij ))+1.

Пусть R_i – деревья с корнями в вершинах v_i. Высота дерева R_i равна либо h(T_i)+1 либо h(T_i)+2. h(R_i) строго возрастают.

Покажем по индукции , что высота дерева S_j равна либо h(R_ij), либо h(R_ij)-1, либо h(R_ij)-2. Пусть данное свойство выполнено для l<j, тогда

h(S_j )=MAX(h(S_j-1),h(T_ij )) | MAX(h(S_j-1),h(T_ij ))+1 следовательно

h(S_j )= MAX(h(S_j-1),h(R_ij) -1) | MAX(h(S_j-1),h(R_ij) -2) |

MAX(h(S_j-1),h(R_ij) -1)+1 | MAX(h(S_j-1),h(R_ij) -2)+1 следовательно по индукции

h(S_j )= (h(R_ij) -1) | ((h(R_ij) -1) | h(R_ij) -2) |

h(R_ij) | (h(R_ij) | h(R_ij) -1) следовательно

h(S_j )= h(R_ij) | (h(R_ij) -1) | (h(R_ij) -2)

Здесь под вертикальной чертой подразумевается разделение возможных вариантов.

Время работы всего алгоритма

T=O(|h(T₀)- h(T_i1 )|+1 +| h(S₁)- h(T_i2 )|+1 +…+| h(S_K-1) - h(T_iK )|+1)=

=O(|h(T₀)- h(T_{i1 )}| +| h(S₁)- h(T_i2 )| +…+| h(S_K-1) - h(T_iK )|)+O(h)=

=O(|h(T₀ )- h(R_i1 )|+4 +| h(R_i1 )- h(R_i2 )|+4 +…+| h(R_i(K-1) ) - h(R_iK )|+4)+O(h)=

(в силу возрастания h(R_i) )

=O(|h(T₀ )- h(R_i1 )|+| h(R_i1 )- h(R_i2 )|+…+| h(R_i(K-1) ) - h(R_iK )|)+O(h)= O(h)

Т.о. T= O(h)=O(log₂ N), где N – количество вершин в суммарном дереве.

Итак, верна следующая

Теорема. Для данной вершины v сбалансированного дерева поиска T разбиение на два сбалансированных дерева поиска T₁ и T₂ таких, что все элементы в T₁ меньше или равны v, и все элементы в T₂ больше или равны v. может быть произведено указанным алгоритмом за время = O(log₂ N), где N – суммарное количество вершин в деревьях T₁ и T₂.