Диаграмма Вороного. Триангуляция Делоне.

Определение. Рассмотрим множество точек {A₁ ,…, A_N } на плоскости. Диаграммой Вороного называется разбиение плоскости на множества {P₁ ,…, P_N}, где P_i состоит из точек, более близких к A_i , чем к остальным точкам из множества {A₁ ,…, A_N }. Будем называть A_i центром области P_i.

Легко увидеть, что для двух точек A₁ и A₂ диаграммой Вороного будет разбиение плоскости на две полуплоскости прямой, являющейся серединным перпендикуляром к [A₁ , A₂ ]. В общем случае (для произвольного конечного множества {A₁ ,…, A_N } ) P_i представляет собой пересечение полуплоскостей, образованных серединным перпендикуляром ко всем отрезкам [A_i , A_j ] (i≠j), содержащих A_i. Отсюда непосредственно вытекает, что P_i является выпуклым многоугольником.

Будем считать диаграмму Вороного построенной, если нам известны:

1)массив вершин всех многоугольников Вороного,

2)массив ребер всех многоугольников Вороного (для каждого ребра задаются номера вершин)

3)массив многоугольников Вороного (для каждого многоугольника задается номер вершины его центра и массив номеров ребер),

4)для каждого ребра многоугольника Вороного номера многоугольников, для которых данное ребро является общим.

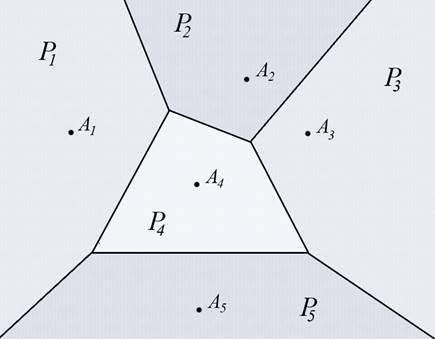
Рис 1. Многоугольники {P₁,…,P₅} диаграммы Вороного точек {A₁,…,A₅}

Теорема 6. В рамках алгоритмов, основанных на сравнениях, j(N)=O(N log N) является нижней оценкой времени решения задачи диаграммы Вороного множества точек {A₁ ,…, A_N }.

Для доказательства данной теоремы покажем, что задача сортировки сводится за линейное время к задаче построения диаграммы Вороного. Рассмотрим множество чисел {x₁ ,…, x_N }. Для решения задачи сортировки данного множества чисел разместим эти числа на оси (OX) числовой плоскости. Решим задачу построения диаграммы Вороного полученного множества точек {(x₁ ,0)…,( x_N ,0)}. Ребрами диаграммы Вороного будут прямые, являющиеся серединными перпендикулярами отрезков, соединяющих соседние числа на оси (OX) в отсортированном множестве чисел {x₁ ,…, x_N }. За линейное время мы можем найти минимальное x_i. Для сортировки множества чисел каждое следующее x_j находится по предыдущему x_i очевидным образом: ищется многоугольник Вороного P_j (=полоса), смежный к многоугольнику P_i. Мы можем это сделать за постоянное время, поскольку у каждого многоугольника есть всего два ребра, а для каждого ребра мы знаем номера двух многоугольников, для которых данное ребро является общим.

Т.о. мы показали, что задача сортировки за линейное время сводится к задаче построения диаграммы Вороного.

¢

Везде далее мы будем предполагать, что наши рассматриваемые точки {A₁ ,…, A_N } имеют общее положение, имея под этим в виду, что никакие четыре точки из рассматриваемого множества не лежат на одной окружности. Данное предположение избавляет нас от рассмотрения большого количества частных случаев (несомненно, в реальных алгоритмах эти случаи рассматривать приходится).

Докажем несколько свойств Диаграммы Вороного (напомним, что везде далее мы предполагаем, что точки имеют общее положение).

Теорема 8. Каждое ребро e многоугольника Вороного P_i лежит на серединном перпендикуляре к отрезку, соединяющему A_i и центр второго многоугольника Вороного, для которого e также является ребром.

Из построения многоугольников Вороного сразу вытекает, что каждое ребро e многоугольника Вороного P_i лежит на серединном перпендикуляре к отрезку, соединяющему A_i и некоторую другую точку A_j из множества {A₁ ,…, A_N }. Рассмотрим A_k – центр второго многоугольника Вороного, для которого e также является ребром. Опять же по построению, ребро e лежит на серединном перпендикуляре к отрезку, соединяющему A_k и некоторую другую точку A_l (см. Рис.2).

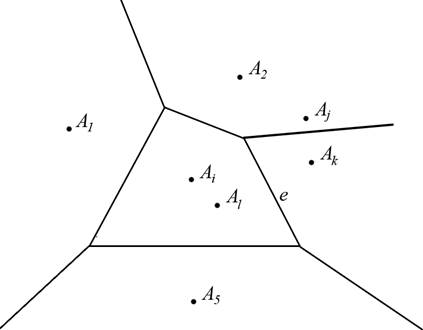
Рис 2. e – серединный перпендикуляр к отрезкам [A_i, A_j] и [A_k, A_l]

Если предположить, что A_j не совпадает с A_k, то мы сразу получаем что все четыре точки A_i, A_j, A_k, A_l лежат на одной окружности, что противоречит общему расположению точек. Стоит отметить, что использование в доказательстве требования общего положения точек не честно, т.к. все можно доказать без него.

¢

Теорема 9. В каждую вершину многоугольника Вороного приходит ровно три ребра.

По теореме 8 получаем, что каждый отрезок диаграммы Вороного лежит на серединном перпендикуляре к отрезку, соединяющему центры многоугольников Вороного, для которых данный отрезок является ребром. Отсюда сразу вытекает, что центры данных многоугольников равноудалены от точки пересечения ребер X. Т.о. если в точку X сходится более трех ребер, то сразу получаем противоречие с общим положением точек. Если же ребер только два, то сразу получаем, что это ребра соответствуют одним и тем же двум многоугольникам Вороного, но тогда эти ребра должны лежать на одной прямой. Это утверждение завершает доказательство.

¢

Теорема 10. Каждая вершина многоугольника Вороного является центром окружности, проходящей через три точки исходного множества {A₁ ,…, A_N }, при этом ни одна из точек множества {A₁ ,…, A_N } не лежит внутри данной окружности.

То, что каждая вершина X многоугольника Вороного является центром окружности, проходящей через три точки исходного множества, следует из теоремы 9 и ее доказательства. Допустим, внутрь данной окружности попала некоторая точка из {A₁ ,…, A_N }. Это не центр многоугольников Вороного A_i1 , A_i2 , A_i3 ,, для которых ребра, сходящиеся в X, являются ребрами (центры этих многоугольников лежат НА окружности). Но если это некоторая другая точка A_j, то получается, что она ближе к X, чем центры A_i1 , A_i2 , A_i3. Но это противоречит тому, что точка X ближе к центрам A_i1 , A_i2 , A_i3, чем к остальным точкам.

¢

Теорема 11. Многоугольники Вороного с центрами, лежащими на выпуклой оболочке исходного множества точек, бесконечны. Других бесконечных многоугольников Вороного нет.

Пусть точка X является вершиной многоугольника выпуклой оболочки. Проведем через нее прямую l такую, что вся выпуклая оболочка лежит по одну сторону прямой. Построим луч r, выходящий из X, перпендикулярный l, лежащий в другой полуплоскости, относительно l, чем точки исходного множества (см. Рис. 3). Не представляет труда доказать, что для всех точек этого луча R точка X находится ближе, чем все остальные точки из {A₁ ,…, A_N }.

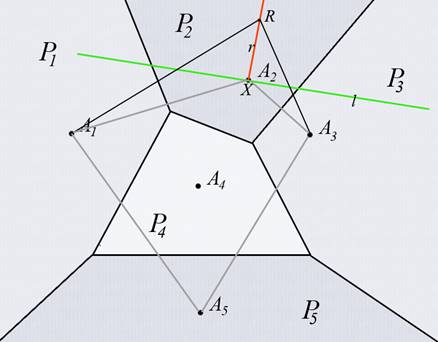
Рис 3. X является ближайшей точкой к R среди точек {A₁,…,A₅}

Отсюда вытекает, что весь луч принадлежит многоугольнику Вороного точки X, следовательно, этот многоугольник бесконечный.

Пусть точка X находится внутри выпуклой оболочки точек {A₁ ,…, A_N }. Рассмотрим последовательность вершин выпуклой оболочки исходного множества точек {B₁ ,…, B_k } и последовательность лучей {(X,B₁) ,…, (X,B_k) }. Углы между соседними лучами в этой последовательности <180. Рассмотрим многоугольник T = пересечению полуплоскостей, образованных серединными перпендикулярами к отрезкам {[X,B₁] ,…, [X,B_k] }, содержащими точку X. Многоугольник Вороного точки X принадлежит T, но T является конечным многоугольником, т.к. все его углы между всеми его ребрами <180 (легко показать, что угол между соседними ребрами многоугольника T = 180-угол между соответствующими лучами [X,B_k] и [X,B_k+1]). Следовательно, многоугольник Вороного точки X тоже конечный.

¢

Определение. Триангуляцией по заданному набору точек {A₁ ,…, A_N } называется разбиение выпуклой оболочки множества точек {A₁ ,…, A_N } на непересекающиеся по внутренности треугольники таким образом, чтобы множество вершин треугольников совпадало бы с множеством точек {A₁ ,…, A_N }.

Теорема 12. Рассмотрим множество треугольников, образованных тройками точек из {A₁ ,…, A_N }, являющимися центрами многоугольников Вороного, имеющими одну общую вершину. Данное множество треугольников дает триангуляцию выпуклой оболочки множества точек {A₁ ,…, A_N } (Делоне 1934).

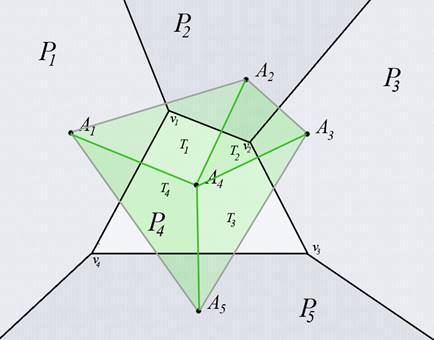
Рис 4. Многоугольники {P₁,…,P₅} диаграммы Вороного точек {A₁,…,A₅} и треугольники {T₁,T₂,T₃,T₄} , соответствующие вершинам многоугольников Вороного {v₁,v₂,v₃,v₄}

Для доказательства теоремы нам надо доказать следующие утверждения: 0)треугольники T_i не вырождены (т.е. точки треугольника не лежат на одной прямой); 1)треугольники T_i не пересекаются по внутренности; 2)для любой точки X, принадлежащей выпуклой оболочке точек {A₁,…,A₅}, существует треугольник T_i : XÎT_i . Докажем данные утверждения.

0)Если вершины A, B, C некоторого треугольника T_i лежат на одной прямой, то серединные перпендикуляры к ним параллельны, что противоречит наличию точки их пересечения v_i.

1)Докажем, что два любых треугольника T_i,T_j не пересекаются по внутренности. Рассмотрим окружности, описанные вокруг этих треугольников, O_i,O_j с центрами в v_i,v_j. Эти окружности не могут быть одна внутри другой, т.к. это сразу противоречило бы теореме 10. Тогда, если окружности не пересекаются, или пересекаются по одной точке, то треугольники T_i,T_j не пересекаются по внутренности. Осталось рассмотреть случай, когда эти окружности пересекаются по двум точкам Q₁, Q₂.

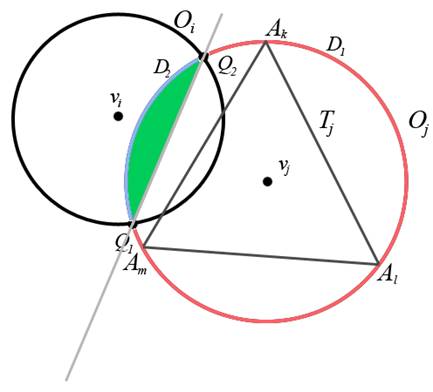
Рис 5. Две вершины диаграммы Вороного v_i,v_j с окружностями O_i,O_j, описанными вокруг вершин соответствующих вершинам v_i,v_j треугольников T_i,T_j.

Покажем, что треугольник T_j ( =D(A_k,A_l,A_m) ), соответствующий вершине диаграммы Вороного v_j, может лежать только по одну сторону от прямой (Q₁,Q₂). Из этого и аналогичного факта для треугольника T_i сразу вытекает, что треугольники T_i, T_j лежат по разные стороны от (Q₁,Q₂) и, следовательно, они не имеют общих внутренних точек. Пусть окружность O_j состоит из двух дуг D₁,D₂, разделенных точками Q₁,Q₂ (см. Рис. 5). Вершины треугольника D(A_k,A_l,A_m) не могут лежать на открытой дуге D₂, т.к. это противоречило бы теореме 10. Но тогда A_k,A_l,A_m лежат по одну сторону от прямой (Q₁,Q₂) и, следовательно, весь треугольник D(A_k,A_l,A_m) лежит по одну сторону от прямой (Q₁,Q₂).

2)Пусть точка x принадлежит внутренности выпуклой оболочки множества точек {A₁, ,A₂… } и не принадлежит ни одному треугольнику T_i.

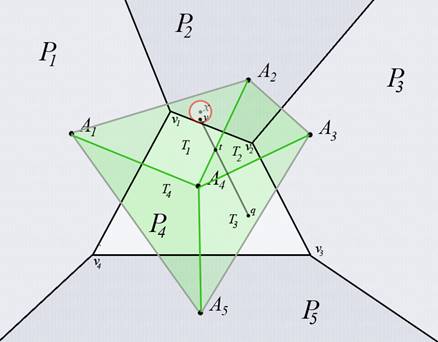
Рис 6. Пусть точка x принадлежит внутренности выпуклой оболочки множества точек {A₁,…,A₅} и не принадлежит ни одному треугольнику T_i.

Тогда и некоторая окрестность O(x) точки x принадлежит выпуклой оболочке множества точек {A₁,A₂,A₃…} и не пересекается ни с одним треугольником T_i. Рассмотрим произвольный треугольник из множества {T₁,T₂,T₃…}. Например (см. Рис. 6) это – T₃. Выберем в нем произвольную точку q. Выберем в O(x) такую точку y, что ни одна из точек {A₁,A₂,A₃…} не лежит на прямой (q,y).

q принадлежит T₃, y не принадлежит ни одному треугольнику T₁,T₂,T₃… . Тогда на [q,y] найдется последняя точка t, принадлежащая одному из T₁,T₂,T₃…. Пусть этот последний треугольник называется T₂ , а точка tÎ[A₂,A₄]. Исходя из предположения, получаем, что интервал (t,y) не пересекается с множеством треугольников {T₁,T₂,T₃…}. [A₂,A₄] не лежит на границе выпуклой оболочки множества точек {A₁,…,A₅}, т.к. по обе его стороны есть точки из выпуклой оболочки (например, y и A₃). Но тогда ребро диаграммы Вороного, выходящее из v₂, перпендикулярное [A₂,A₄] должно быть конечным (по теореме 11). Пусть оно завершается в точке v₁. Но тогда треугольник T₁ опирается на отрезок [A₂,A₄] и начало отрезка [t,y] обязано принадлежать T₁. А это противоречит тому, что интервал (t,y) не пересекается с множеством треугольников {T₁,T₂,T₃…}.

¢

Классическое построение диаграммы Вороного осуществляется методом деления пополам. Основная идея алгоритма сводится к тому, что множество точек {A₁,A₂,A₃…}, по которому строится диаграмма Вороного, разбивается на две [почти] равные части с помощью разбиения точек по оси абсцисс. Для каждой части запускается тот же алгоритм построения диаграммы Вороного, а потом предъявляется алгоритм объединения этих двух диаграмм Вороного в диаграмму всего множества точек за линейное время. Мы не будем описывать подробности данного алгоритма, но если поверить, что указанные действия можно осуществить, то мы сразу получаем теорему о верхней оценке времени решения задачи построения диаграммы Вороного.

Теорема 13. В рамках алгоритма, основанных на сравнениях, диаграмму Вороного множества точек {A₁ ,…, A_N } можно построить за время O(N log N), что является верхней оценкой времени решения данной задачи в рамках алгоритмов, основанных на сравнениях.

Определение. Триангуляцией Делоне множества точек {A₁ ,…, A_N } называется такая триангуляция множества точек {A₁ ,…, A_N }, что для любого треугольника триангуляции T описанная вокруг него окружность не содержит внутри никаких точек из множества {A₁ ,…, A_N }.

Теорема 14. Для любого множества точек {A₁ ,…, A_N } триангуляцией Делоне существует. Для случая общего расположения точек {A₁ ,…, A_N } триангуляцией Делоне единственна.

Существование триангуляции Делоне мы доказали (на самом деле, существование мы доказали для общего расположения точек, но существование есть и в общем случае). Единственность триангуляции Делоне следует из взаимно-однозначного соответствия между триангуляцией Делоне и диаграммой Вороного. Мы доказали это соответствие только в одну сторону. В обратную сторону доказательство проводиться не будет. Но единственность триангуляции Делоне можно доказать с помощью другого подхода.

Лемма 1. Рассмотрим произвольную окружность (x-a)²+(y-b)²=r² на плоскости XY. Вертикальная проекция данной окружности на стандартный параболоид z=x²+y² лежит в одной плоскости. Все точки внутри окружности проецируются в точки, лежащие ниже данной плоскости, а точки снаружи окружности – в точки выше данной плоскости.

Распишем уравнение окружности: x²+y²-2ax-2by=r²-a²-b². При проектировании этой окружности на параболоид x²+y² можно заменить на z. После чего мы получим уравнение точек, лежащих в одной плоскости: -2ax-2by+z=r²-a²-b².

Если некоторая (x₁,y₁) точка лежит внутри данной окружности, то для нее выполняется соотношение (x-a)²+(y-b)²=p², где p<r. Но тогда проекция данной точки на параболоид удовлетворяет соотношению x₁²+y₁²-2ax₁-2by₁=p²-a²-b² , и следовательно 2ax₁-2by₁+z₁=p²-a²-b². Откуда сразу получаем z₁<z, где z удовлетворяет соотношению 2ax₁-2by₁+z=r²-a²-b². Т.е. проекция точки, лежащей внутри окружности, находится ниже плоскости, в которой лежит окружность. Доказательство для точек вне окружности аналогично. Ч.Т.Д.

Рассмотрим триангуляцию Делоне нашего множество точек на плоскости {A₁,A₂,A₃…} и вертикальную проекцию вершин этой триангуляции на стандартный параболоид z=x²+y². Вершины триангуляции лежат на параболоиде. Ребра триангуляции лежат сверху параболоида. Окружность, описанная вокруг любого треугольника T данной триангуляции, не содержит внутри других точек из множества {A₁,A₂,A₃…}. Отсюда из леммы 1 сразу следует, что все проекции всех остальных точек {A₁,A₂,A₃…} на параболоид лежат с верхней стороны от плоскости, проходящей через проекцию вершин T на параболоид. Но тогда получается, что объединение треугольников, вершины которых являются проекциями вершин треугольников триангуляции Делоне, дает нижнюю половину выпуклой оболочки проекций {A₁,A₂,A₃…} на параболоид. А поскольку выпуклая оболочка единственна, то мы сразу получаем единственность триангуляции Делоне.

¢

Можно много говорить о значимости триангуляции Делоне и диаграммы Вороного. Например, диаграмма Вороного дает наиболее разумный способ определения кусочно-постоянной интерполяции функции для отображения R²→R. Другой хороший пример: если использовать утверждение о том, что для триангуляции количество ребер равно O(n), где n – количество вершин триангуляции (это утверждение мы будем доказывать, когда будем рассматривать алгоритмы на графах), то за линейное время легко свести задачу поиска всех ближайших соседей в множестве точек {A₁ ,…, A_N } к задаче построения диаграммы Вороного множества точек {A₁ ,…, A_N }. Триангуляция Делоне дает хорошую формализацию понятия соседних вершин в множестве точек {A₁ ,…, A_N }. И т.д.